题目内容
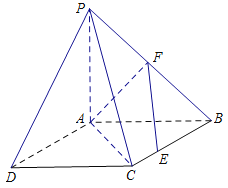
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】(Ⅰ)由条件可知四边形![]() 为平行四边形(菱形),则
为平行四边形(菱形),则![]() 与
与![]() 的交点
的交点![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 的中点,根据线面平行判定定理,问题可得证;(Ⅱ)由题意,通过计算证明可得,
的中点,根据线面平行判定定理,问题可得证;(Ⅱ)由题意,通过计算证明可得,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,且三角形
,且三角形![]() 是以
是以![]() 为直角的直角三角形,从而可求线段
为直角的直角三角形,从而可求线段![]() 的长.
的长.
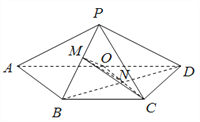
试题解析:(Ⅰ)连接![]() 交
交![]() 与
与![]() ,连接
,连接![]() .
.
因为![]() 为
为![]() 的中点,
的中点,![]() ,所以
,所以![]() .
.
又因为![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() 为
为![]() 的中点,因为
的中点,因为![]() 为
为![]() 的中点, 所以
的中点, 所以![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)由四边形![]() 为平行四边形,知
为平行四边形,知![]() ,
,
所以![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
所以![]() ,即
,即![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 为
为![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() ,
,
所以![]() .
.

【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 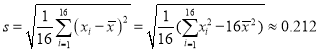 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)判断是否有![]() 的把握认为学生的学习积极性与对待班级工作的态度有关系?
的把握认为学生的学习积极性与对待班级工作的态度有关系?
附:  , n=a+b+c+d.
, n=a+b+c+d.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
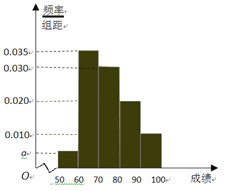
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?