题目内容
10.过抛物线y2=4x的顶点作互相垂直的两条弦OA、OB,求AB中点的轨迹方程.分析 设直线OA的方程为y=kx(k≠0),代入抛物线方程,求得交点A,再设出直线OB的方程,可得交点B,再由中点坐标公式,运用平方消元,即可得到中点的轨迹方程.
解答 解:∵依题意可知直线OA的斜率存在且不为0,
∴设直线OA的方程为y=kx(k≠0),
∴联立y2=4x,解得xA=$\frac{4}{{k}^{2}}$,yA=$\frac{4}{k}$,
以-$\frac{1}{k}$代上式中的k,解方程组,
解得xB=4k2,yB=-4k
∴A($\frac{4}{{k}^{2}}$,$\frac{4}{k}$),B(4k2,-4k),
设AB中点M(x,y),则由中点坐标公式,
得x=$\frac{1}{2}$($\frac{4}{{k}^{2}}$+4k2),y=$\frac{1}{2}$($\frac{4}{k}$-4k),
消去参数k,得y2=2x-8,即为AB中点的轨迹方程.
点评 本题考查抛物线的方程和性质,主要考查直线和抛物线方程联立,求交点,同时考查两直线垂直的条件:斜率之积为-1,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
20.已知p:不等式|x+1|+|x-2|>m的解集为R;q:f(x)=log(5-2m)x为减函数,则p成立是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.若角α的终边经过点$(\sqrt{5},-2)$,则sinα等于多少( )
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $-\frac{2}{3}$ | D. | $-\frac{{\sqrt{5}}}{3}$ |
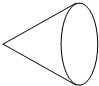
5.下图所示的圆锥的俯视图为( )

| A. | 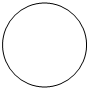 | B. | 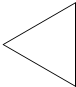 | C. |  | D. |  |
15.如果椭圆的两焦点为F1(-1,0)和F2(1,0),P是椭圆上的一点,且|PF1|、|F1F2|、|PF2|成等差数列,那么椭圆的方程是( )
| A. | $\frac{x^2}{3}+\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | C. | $\frac{x^2}{16}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{16}+\frac{y^2}{12}$=1 |