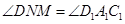题目内容
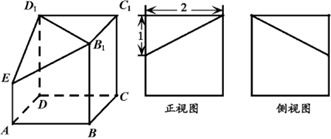
(本小题满分12分)一个四棱锥的直观图和三视图如图所示: 

(1)求证: ⊥
⊥ ;
;
(2)求出这个几何体的体积。
(3)若在PC上有一点E,满足CE:EP=2:1,求证PA//平面BED。
(1)∵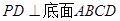 ,
,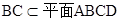
∴ 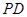 ⊥
⊥ , 在梯形
, 在梯形 中,
中,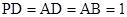 ,
,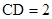
∴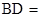
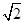 ,又可得
,又可得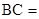
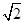 ,
,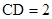 ,∴
,∴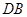 ⊥
⊥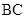 ,
,
又∵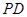
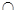
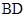
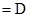 ,
,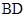 ,
,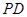
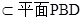 ∴
∴ ⊥面
⊥面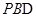 ,
,
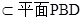
∴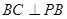
(2)4;(3)连结AC,设AC交BD于O点,  CD//AB,CD=2AB,
CD//AB,CD=2AB,
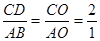
又
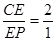
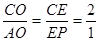 ,
, PA//EO,
PA//EO,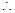 PA//平面BED
PA//平面BED
解析试题分析:由三视图可知: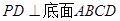 ,底面ABCD为直角梯形,,
,底面ABCD为直角梯形,,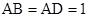 ,
,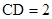 ,(1)∵
,(1)∵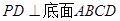 ,
,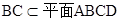
∴ 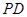 ⊥
⊥ , 在梯形
, 在梯形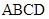 中,
中,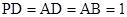 ,
,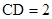
∴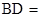
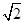 ,又可得
,又可得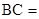
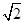 ,
,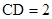 ,
,
∴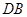 ⊥
⊥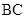 ,
,
又∵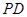
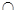
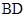
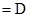 ,
,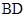 ,
,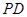
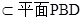
∴ ⊥面
⊥面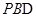 ,
,
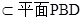
∴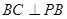
(2)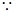 PD
PD 平面ABCD,
平面ABCD, PD是这个四棱锥的高,又底面
PD是这个四棱锥的高,又底面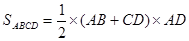
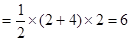 ,所以
,所以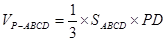
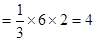
(3)连结AC,设AC交BD于O点,  CD//AB ,CD=2AB,
CD//AB ,CD=2AB,
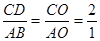
又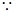
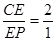
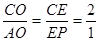 ,
,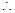 PA//EO,EO
PA//EO,EO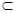 平面BED ,PA
平面BED ,PA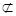 平面BE
平面BE 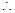 PA//平面BED
PA//平面BED
考点:本题考查了空间中的线面关系及体积的求法
点评:高考中常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理.

练习册系列答案
相关题目
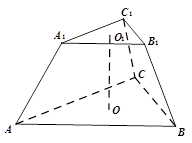
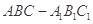 中,
中,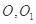 分别是上、下底面的中心.已知
分别是上、下底面的中心.已知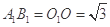 ,
,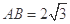 .
.
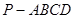 中,底面
中,底面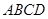 为平行四边形,
为平行四边形,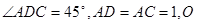 为
为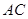 中点,
中点,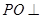 面
面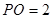 ,
, 为
为 中点。
中点。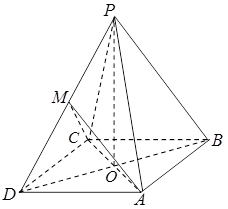
 面
面 。
。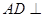 面
面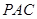 。
。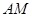 与平面
与平面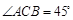 ,
,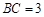 ,过动点A作
,过动点A作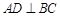 ,垂足
,垂足 在线段
在线段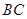 上且异于点
上且异于点 ,连接
,连接 ,沿
,沿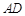 将△
将△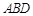 折起,使
折起,使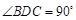 (如图2所示).
(如图2所示). 
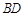 的长为多少时,三棱锥
的长为多少时,三棱锥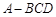 的体积最大;
的体积最大;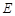 ,
,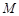 分别为棱
分别为棱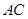 的中点,试在棱
的中点,试在棱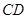 上确定一点
上确定一点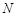 ,使得
,使得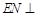
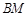 ,并求
,并求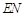 与平面
与平面 所成角的大小.
所成角的大小. 的最大面积及相应的x值.
的最大面积及相应的x值.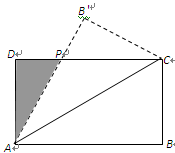
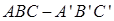 中,
中,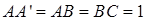 ,
,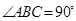 .棱
.棱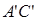 上有两个动点E,F,且EF =" a" (a为常数).
上有两个动点E,F,且EF =" a" (a为常数).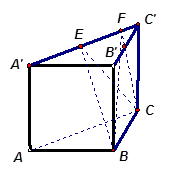
 的正方体
的正方体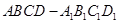 中,M,N分别是棱CD,AD的中点。(1)求证:四边形
中,M,N分别是棱CD,AD的中点。(1)求证:四边形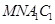 是梯形;(2)求证:
是梯形;(2)求证: