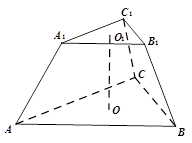
题目内容
正三棱台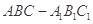 中,
中,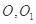 分别是上、下底面的中心.已知
分别是上、下底面的中心.已知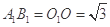 ,
,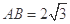 .
.
(1)求正三棱台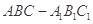 的体积;
的体积;
(2)求正三棱台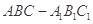 的侧面积.
的侧面积.
(1)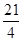 ;(2)
;(2)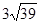
解析试题分析:本题关于空间几何体的侧面积和体积的计算,该类题要注意以下两点:
圆柱、圆锥、圆台的侧面积和体积,主要依靠公式来解决,但其侧面积公式的推导思路要理解领会,是将空间几何体的表面展开,“化曲为直”,将空间问题转化为平面问题解决.
圆台、棱台的表面积和体积公式的推导及有关计算,如果不能直接利用公式,要记住“还台为锥”,化难为易.
(1)因为上下底面边长、高知道,所以可求上下底面面积,直接带入公式可解;(2)由已知条件可求斜高,所以每个侧面的面积可求,然后乘以3,即侧面积.
试题解析:(1)正三棱台 的上底面积为
的上底面积为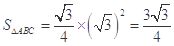 2分
2分
下底面积为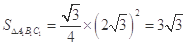 4分
4分
所以正三棱台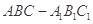 的体积为
的体积为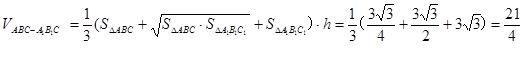
 7分
7分
(2)设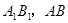 的中点分别为
的中点分别为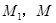
则正三棱台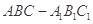 的斜高
的斜高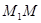 =
=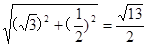 10分
10分
则正三棱台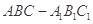 的侧面积
的侧面积 14分
14分
考点:空间几何体的体积、侧面积计算.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 的底面边长为
的底面边长为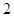 ,侧棱长为
,侧棱长为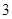 ,
,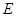 为棱
为棱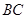 的中点.
的中点.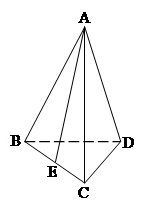
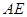 与
与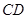 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);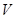 .
.
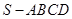 中,侧棱
中,侧棱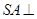 底面
底面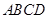 ,且底面
,且底面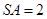 ,
,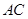 与
与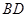 相交于点
相交于点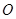 .
.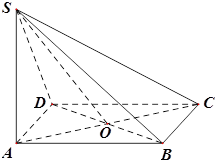
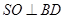 ;
;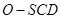 的体积.
的体积.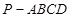 的底面是正方形,
的底面是正方形,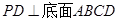 ,点
,点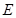 在棱
在棱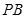 上.
上.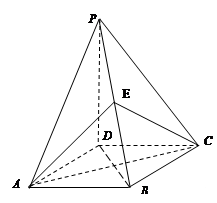
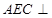 平面
平面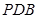 ;
;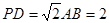 ,且
,且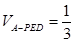 时,确定点
时,确定点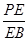 的值.
的值. ,BD=CD=1,另一个侧面ABC是正三角形.
,BD=CD=1,另一个侧面ABC是正三角形.
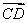 的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)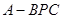 中,
中,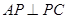 ,
,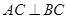 ,
,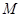 为
为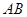 中点,
中点,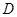 为
为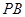 中点,且
中点,且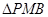 为正三角形。
为正三角形。
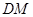 //平面
//平面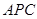 ;
;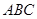 ⊥平面
⊥平面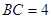 ,
,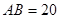 ,求三棱锥
,求三棱锥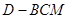 的体积.
的体积.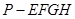 ,下半部分是长方体
,下半部分是长方体 。图2、图3分别是该标识墩的正(主)视图和俯视图。
。图2、图3分别是该标识墩的正(主)视图和俯视图。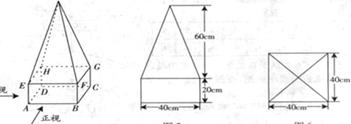


 ⊥
⊥ ;
;