题目内容
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为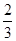 .
.
(1)求乙至多击中目标2次的概率;
(2)记甲击中目标的次数为Z,求Z的分布列、数学期望和标准差.
(1) (2) Z的分布列如下表:
(2) Z的分布列如下表:Z 0 1 2 3 P 
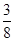
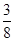



解析解:(1)甲、乙两人射击命中的次数服从二项分布,故乙至多击中目标2次的概率为1-C33 3=
3= .
.
(2)P(Z=0)=C30 3=
3= ;
;
P(Z=1)=C31 3=
3=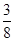 ;
;
P(Z=2)=C32 3=
3=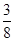 ;
;
P(Z=3)=C33 3=
3= .
.
Z的分布列如下表:
E(Z)=0×Z 0 1 2 3 P 
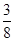
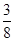

 +1×
+1×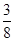 +2×
+2×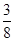 +3×
+3× =
= ,
,
D(Z)= 2×
2× +
+ 2×
2×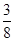 +
+ 2×
2×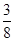 +
+ 2×
2× =
= ,∴
,∴ =
= .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| | | | | | |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(2)在该样本的一等品中,随机抽取2件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.

 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率. ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.



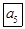 ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为 ,出现1的概率为
,出现1的概率为 .记X=a1+a2+a3+a4+a5,当程序运行一次时,
.记X=a1+a2+a3+a4+a5,当程序运行一次时, 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 和
和 ,试求:
,试求: