题目内容
若一批白炽灯共有10000只,其光通量X服从正态分布,其正态分布密度函数是f(x)= ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
(1)(203,215);(2)(191,227).
(1) 6826 (2) 9974
解析解:由于X的正态分布密度函数为
f(x)=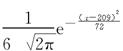 ,x∈(-∞,+∞),
,x∈(-∞,+∞),
∴μ=209,σ=6.
∴μ-σ=209-6=203,μ+σ=209+6=215.
μ-3σ=209-6×3=209-18=191,
μ+3σ=209+6×3=209+18=227.
因此光通量X的取值在区间(203,215),(191,227)内的概率应分别是0.6826和0.9974.
(1)于是光通量X在(203,215)范围内的灯泡个数大约是10000×0.6826=6826.
(2)光通量在(191,227)范围内的灯泡个数大约是10000×0.9974=9974.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
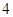 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 .
. ,
, 的值;
的值; 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率; ,求随机变量
,求随机变量 .
.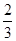 ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时:
.记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时: ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,求随机变量
,求随机变量