题目内容
某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布律和数学期望.
的分布律和数学期望.
(1) ;
;
(2)随机变量 的分布列为:
的分布列为:

10 20 30 40 





 .
.
解析试题分析:(1)这属于一个古典概型问题,可以考虑摸2次,总的方法数为 ,而摸2次后停止摸奖,说明第一次不是黑球,而第2次摸的是黑球,有
,而摸2次后停止摸奖,说明第一次不是黑球,而第2次摸的是黑球,有 种可能,因此所求概率为
种可能,因此所求概率为 ;(2)因为是不放回的摸球,因此得奖金额可能为0元、10元、20元、30元、40元,这样随机变量
;(2)因为是不放回的摸球,因此得奖金额可能为0元、10元、20元、30元、40元,这样随机变量 的分布列就要求出,奖金0元,说明第1次摸的是黑球,奖金10元说明第一次摸的是拍球或黄球,第2次黑球,奖金20元,说明第1次红球,第2次黑球或第1、第2次是白球或黄球,第3次黑球,奖金30元,第1次与第2次里有1次是红球,另一次为白球或黄球,第3次黑球,而奖金40元说明第4次是黑球,由上可计算出名概率计算出分布列,期望.
的分布列就要求出,奖金0元,说明第1次摸的是黑球,奖金10元说明第一次摸的是拍球或黄球,第2次黑球,奖金20元,说明第1次红球,第2次黑球或第1、第2次是白球或黄球,第3次黑球,奖金30元,第1次与第2次里有1次是红球,另一次为白球或黄球,第3次黑球,而奖金40元说明第4次是黑球,由上可计算出名概率计算出分布列,期望.
试题解析:(1)设“1名顾客摸球2次停止摸奖”为事件 ,
,
则  ,(4分)
,(4分)
故1名顾客摸球2次停止摸奖的概率 .
.
(2)随机变量 的所有取值为
的所有取值为 .
.  ,
, ,
,
 ,
, (9分)
(9分)
所以,随机变量 的分布列为:
的分布列为:
(12分)

10 20 30 40 





 .(14分)
.(14分)
考点:(1)古典概型;(2)随机变量分布列与数学期望.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 .
. ,
, 的值;
的值; 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率; ,求随机变量
,求随机变量 .
. ,乙每次击中目标的概率为
,乙每次击中目标的概率为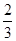 .
.
 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求