题目内容
对某电子元件进行寿命追踪调查,所得情况如右频率分布直方图.
(1)图中纵坐标 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 ;
;
(2)根据图表的数据按分层抽样,抽取 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率.
(1)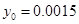 ;(2)应抽取
;(2)应抽取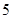 个;(3)
个;(3)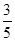 .
.
解析试题分析:本题主要考查频率分布直方图、随机事件的概率等基础知识,考查学生的分析问题解决问题的能力、读图能力、计算能力.第一问,利用所有频率之和为1,利用“高=频率÷组距”计算 ;第二问,利用“频率=频数÷样本总数”计算寿命为
;第二问,利用“频率=频数÷样本总数”计算寿命为 之间应抽取的个数;第三问,分别设出寿命为
之间应抽取的个数;第三问,分别设出寿命为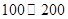 之间的2个元件和
之间的2个元件和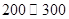 之间的3个元件,先写出从5个元件中任取2个元件的所有情况,再从中选出符合题意的种数,两个种数相除得到概率的值.
之间的3个元件,先写出从5个元件中任取2个元件的所有情况,再从中选出符合题意的种数,两个种数相除得到概率的值.
试题解析:(1)根据题意: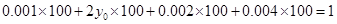
解得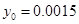 3分
3分
(2)设在寿命为 之间的应抽取
之间的应抽取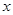 个,根据分层抽样有:
个,根据分层抽样有: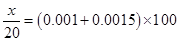 5分
5分
解得: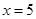
所以应在寿命为 之间的应抽取
之间的应抽取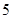 个 7分
个 7分
(3)记“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”为事件
”为事件 ,由(2)知
,由(2)知
寿命落在 之间的元件有
之间的元件有 个分别记
个分别记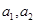 ,落在
,落在 之间的元件有
之间的元件有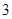 个分别记为:
个分别记为: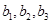 ,从中任取
,从中任取 个球,有如下基本事件:
个球,有如下基本事件: 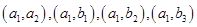 ,
,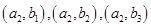 ,
, 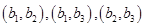 ,共有
,共有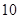 个基本事件 9分
个基本事件 9分
事件 “恰好有一个寿命为
“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”有:
”有: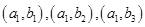 ,
,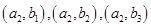 共有
共有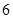 个基本事件 10分
个基本事件 10分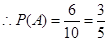 11分
11分
答:事件“恰好有一个寿命为 ,另一个寿命为
,另一个寿命为 ”的概率为
”的概率为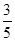 . 12分
. 12分
考点:频率分布直方图、随机事件的概率.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
| 答对题目数 |  | 8 | 9 |  |
| 女 | 2 | 13 | 12 | 8 |
| 男 | 3 | 37 | 16 | 9 |
(2)从答对题目数少于8的出租车司机中任选出两人做进一步的调查,求选出的两人中至少有一名女出租车司机的概率.
某小组共有A、B、C、D、E五位同学,他们的身高(单位:m)以及体重指标(单位:kg/m2)如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是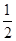 ;
; 巷道有
巷道有 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为 .
.
 ,求
,求 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.  位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 .
. ,
, 的值;
的值; 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率; ,求随机变量
,求随机变量 .
. ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时:
.记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时: ,乙每次击中目标的概率为
,乙每次击中目标的概率为