题目内容
将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第2个数为
.
n2-n+3
n2-n+3
.
|
分析:首先由三角形数阵,知第n行的前面共有1+2+3+…+(n-1)个连续奇数,第n行从左向右的第2个数应为 2{
+2}-1,即可得到答案.
| n(n-1) |
| 2 |
解答:解:观察三角形数阵,知第n行(n≥3)前共有1+2+3+…+(n-1)=
个连续奇数,
第n行(n≥3)从左向右的第2个数为
+2个奇数,故其值为2{
+2}-1,即n2-n+3;
故答案为n2-n+3.
| n(n-1) |
| 2 |
第n行(n≥3)从左向右的第2个数为
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
故答案为n2-n+3.
点评:本题从观察数阵的排列规律,考查了数列的应用问题;解题时,关键是发现规律并应用所学知识,来解答问题.

练习册系列答案
相关题目
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第n 行(n≥3)从左向右的第3 个数为( )
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第n 行(n≥3)从左向右的第3 个数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
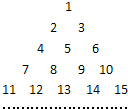 将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为
将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为 将全体正整数排成一个三角形数阵:
将全体正整数排成一个三角形数阵: