题目内容
将全体正整数排成一个三角形数阵:1
3 2
6 5 4
10 9 8 7
…
按照以上排列的规律,第n 行(n≥3)从左向右的第1个数为
分析:先找到数的分布规律,求出第n行结束的时候一共出现的数的个数,即为第n 行(n≥3)从左向右的第1个数.
解答:解:第一行1个数,第二行2个数,一共3个数,第一数为3
第三行3个数,一个6个数,第一个数为6
依此类推第n行结束的时候一共出现的数的个数,即为第n 行(n≥3)从左向右的第1个数
∴第n 行(n≥3)从左向右的第1个数为
故答案为:
第三行3个数,一个6个数,第一个数为6
依此类推第n行结束的时候一共出现的数的个数,即为第n 行(n≥3)从左向右的第1个数
∴第n 行(n≥3)从左向右的第1个数为
| n(n+1) |
| 2 |
故答案为:
| n(n+1) |
| 2 |
点评:本题借助于一个三角形数阵考查了数列的应用,解题的关键是找规律,是道中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第n 行(n≥3)从左向右的第3 个数为( )
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第n 行(n≥3)从左向右的第3 个数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
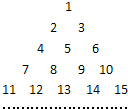 将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为
将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为 将全体正整数排成一个三角形数阵:
将全体正整数排成一个三角形数阵: