Question

【题目】已知定直线l：y=x+3，定点A（2，1），以坐标轴为对称轴的椭圆C过点A且与l相切．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）椭圆的弦AP，AQ的中点分别为M，N，若MN平行于l，则OM，ON斜率之和是否为定值？若是定值，请求出该定值；若不是定值请说明理由．

Answer 1

【答案】解：（Ⅰ）设椭圆的标准方程为mx2+ny2=1（m＞0，n＞0，m≠n） 椭圆C过点A，所以4m+n①，
将y=x+3代入椭圆方程化简得：（m+n）x2+6nx+9n﹣1=0，
因为直线l与椭圆C相切，所以△=（6n）2﹣4（m+n）（9n﹣1）=0②，
解①②可得， ，
所以椭圆方程为 ；
（Ⅱ）设点P（x1 ， y1），Q（x2 ， y2），则有 ，
由题意可知PQ∥MN，所以kPQ=kMN=1，设直线PQ的方程为y=x+t，
代入椭圆方程并化简得：3x2+4tx+2t2﹣6=0
由题意可知 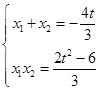③

通分后可变形得到
将③式代入分子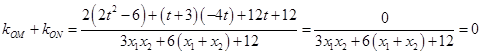
所以OM，ON斜率之和为定值0
【解析】（Ⅰ）设椭圆的标准方程为mx2+ny2=1（m＞0，n＞0，m≠n），椭圆C过点A，所以4m+n①，将y=x+3代入椭圆方程化简得：（m+n）x2+6nx+9n﹣1=0，由△=（6n）2﹣4（m+n）（9n﹣1）=0②， 可得， ，即可得椭圆方程．（Ⅱ）设点P（x1 ， y1），Q（x2 ， y2），可知PQ∥MN，所以kPQ=kMN=1， 设直线PQ的方程为y=x+t，代入椭圆方程并化简得：3x2+4tx+2t2﹣6=0
由题意可知 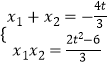，利用韦达定理可计算
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．