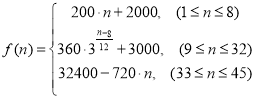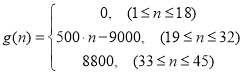题目内容
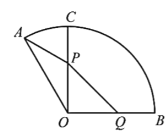
【题目】如图是一个半径为1千米的扇形景点的平面示意图,![]() .原有观光道路OC,且
.原有观光道路OC,且![]() .为便于游客观赏,景点管理部门决定新建两条道路PQ、PA,其中P在原道路OC(不含端点O、C)上,Q在景点边界OB上,且
.为便于游客观赏,景点管理部门决定新建两条道路PQ、PA,其中P在原道路OC(不含端点O、C)上,Q在景点边界OB上,且![]() ,同时维修原道路的OP段,因地形原因,新建PQ段、PA段的每千米费用分别是
,同时维修原道路的OP段,因地形原因,新建PQ段、PA段的每千米费用分别是![]() 万元、
万元、![]() 万元,维修OP段的每千米费用是
万元,维修OP段的每千米费用是![]() 万元.
万元.
(1)设![]() ,求所需总费用
,求所需总费用![]() ,并给出
,并给出![]() 的取值范围;
的取值范围;
(2)当P距离O处多远时,总费用最小.
【答案】(1)![]()
![]() (2)当点P距离O处
(2)当点P距离O处![]() 千米时,总费用的最小
千米时,总费用的最小
【解析】
(1)在![]() 中利用正弦定理将求出
中利用正弦定理将求出![]() ,
,![]() ,代入
,代入![]() 并化简即可求得解析式,再根据P在原道路OC上求出
并化简即可求得解析式,再根据P在原道路OC上求出![]() 的取值范围;(2)求出
的取值范围;(2)求出![]() 的导数,根据导数的符号判断函数的单调性,从而求得最小值.
的导数,根据导数的符号判断函数的单调性,从而求得最小值.
解:(1)因为![]()
![]() ,所以
,所以![]() .
.
又在![]() 中,
中,![]()
![]() ,
,
所以![]()
![]() ,
,
![]()
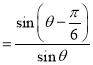
![]() .
.
因为![]() ,
,
所以![]()
![]()
![]()
![]() .
.
(2)![]()
![]() ,
,
由![]() 得
得![]() ,
,
又![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时,![]() 取最小值,此时
取最小值,此时![]() .
.
答:当点P距离O处![]() 千米时,总费用的最小.
千米时,总费用的最小.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目