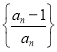
题目内容
【题目】已知函数![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(1)求函数![]() 的最大值与最小值;
的最大值与最小值;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图象;已知点
的图象;已知点![]() ,若函数
,若函数![]() 的图象上存在点
的图象上存在点![]() ,使得
,使得![]() ,求函数
,求函数![]() 图象的对称中心.
图象的对称中心.
【答案】(1)![]() 的最大值为2,最小值为
的最大值为2,最小值为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由行列式运算求出![]() ,由函数图象过两点,求出
,由函数图象过两点,求出![]() ,得函数解析式,化函数式为一个角的一个三角函数式,可求得最值;
,得函数解析式,化函数式为一个角的一个三角函数式,可求得最值;
(2)由图象变换写出![]() 表达式,它的最大值是2,因此要满足条件,只有
表达式,它的最大值是2,因此要满足条件,只有![]() 在
在![]() 图象上,由此可求得
图象上,由此可求得![]() ,结合余弦函数的性质可求得对称中心.
,结合余弦函数的性质可求得对称中心.
(1)易知![]() ,则由条件,得
,则由条件,得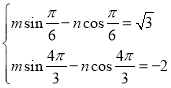 ,
,
解得![]() 故
故![]() .
.
故函数![]() 的最大值为2,最小值为
的最大值为2,最小值为![]()
(2)由(1)可知: ![]() .
.
于是,当且仅当![]() 在
在![]() 的图象上时满足条件.
的图象上时满足条件.
![]() . 由
. 由![]() ,得
,得![]()
故![]() . 由
. 由![]() ,得
,得![]()
于是,函数![]() 图象的对称中心为:
图象的对称中心为:![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目