题目内容
【题目】已知直线l的参数方程为 
（t为参数），曲线C的参数方程为 
（θ为参数）
（1）以原点O为极点，以x轴正半轴为极轴（与直角坐标系xOy取相同的长度单位）建立极坐标系，若点P的极坐标为（4， 
），判断点P与直线l的位置关系；
（2）设点Q是曲线C上的一个动点，利用曲线C的参数方程求Q到直线l的距离的最大值与最小值的差．
【答案】
（1）解：把点P的极坐标（4， 
），转化成直角坐标P（2，2 
），
把直线l的参数方程：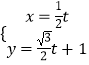 
，化为直角坐标方程为y= x+1，
由于点P的坐标不满足直线l的方程，故P不在直线l上
（2）解：点Q是曲线C上的一个动点，曲线C的参数方程为 
（θ为参数），
曲线C的直角坐标方程为：（x﹣2）2+y2=1，
∴曲线C表示已（2，0）为圆心，1为半径的圆，
圆心到直线的距离为d= 
= + 
，
故点Q到直线l的距离的最小值为d﹣r= ﹣ ，
最大值为d+r= + 
，
∴曲线C的参数方程求Q到直线l的距离的最大值与最小值的差2
【解析】（1）将P的极坐标（4， ），转化成直角坐标P（2，2 ），将参数方程转化成直角坐标，由P点坐标不满足直线l的方程，P不在直线l上；（2）将C的参数方程转化成直角坐标方程，取得圆心坐标及半径，由点到直线记得距离公式求得圆心到直线的距离d，即可求得点Q到直线l的距离的最小值为d﹣r和最大值为d+r，两式相减即可求得结果．
练习册系列答案
一线名师权威作业本系列答案
相关题目
