题目内容
【题目】已知直线l：x﹣y=1与圆M：x2+y2﹣2x+2y﹣1=0相交于A，C两点，点B，D分别在圆M上运动，且位于直线AC两侧，则四边形ABCD面积的最大值为 ．
【答案】
【解析】解：把圆M：x2+y2﹣2x+2y﹣1=0化为标准方程：（x﹣1）2+（y+1）2=3，圆心（1，﹣1），半径r= 
．
直线与圆相交，由点到直线的距离公式的弦心距d= 
= 
，
由勾股定理的半弦长= 
= 
，所以弦长|AB|=2× = 
．
又B，D两点在圆上，并且位于直线AC的两侧，
四边形ABCD的面积可以看成是两个三角形△ABC和△ACD的面积之和，
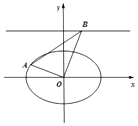
如图所示，
当B，D为如图所示位置，即BD为弦AC的垂直平分线时（即为直径时），
两三角形的面积之和最大，即四边形ABCD的面积最大，
最大面积为：S= 
×|AB|×|CE|+ ×|AB|×|DE|
= 
= ．
所以答案是： ．
练习册系列答案
相关题目
