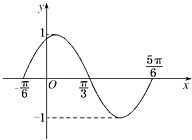
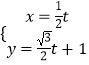题目内容
【题目】已知：关于x的不等式（mx－（m+1））（x－2）>0（m
R）的解集为集合P
（I）当m>0时，求集合P；
（II）若{
}
P，求m的取值范围.
【答案】（I）见解析；（II）
【解析】
（I）通过比较两根大小进行分类讨论，利用二次函数的图像即可得到不等式的解集；
（Ⅲ）依题意，当x∈（-3，2）时，不等式（mx－（m+1））（x－2）>0恒成立，分类讨论即可求出m的范围．
（I）当m>0时，原不等式变为
当0<m<1时，
>2，不等式的解为x<2或
；
当m=1时，=2，不等式的解为x<2或x>2；
当m>1时，<2，不等式的解为x<或x>2；
综上所述，当0<m≤1时，P=（－
，2）
（，+），
当m>l时，P=（－，）（2，+）。
（II）当m>0时，由（I）知，满足{x|－3<x<2}
P，需要0<m≤1；
当m=0时，不等式变为
，则P=（－，2），满足条件；
当m<0时，不等式变为
，此时<2，则P=（，2）
满足{x|－3<x<2}
P，需要≤
，则
，
综上所述：
练习册系列答案
口算题天天练系列答案
相关题目
