Question

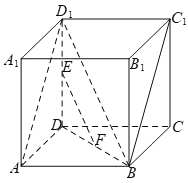
【题目】如图所示，在正方体中，、分别为和的中点．

（1）求证：平面；

（2）求直线与面所成的角的余弦值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）连接，利用中位线的性质证明出，然后利用直线与平面平行的判定定理可证明出平面；

（2）设正方体的棱长为，取的中点，连接，证明出平面，可得出直线与平面所成的角为，然后计算出的三边边长，然后利用锐角三角函数的定义可求出，即为直线与面所成的角的余弦值．

（1）如下图所示，连接，

、分别为和的中点，，

平面，平面，平面；

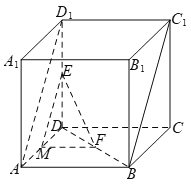
（2）如下图所示，设正方体的棱长为，取的中点，连接，

、分别为、的中点，则，且，

在正方体中，平面，平面，

直线与平面所成的角为，由勾股定理得，

平面，平面，，

，

在中，.

因此，直线与面所成的角的余弦值为.