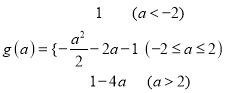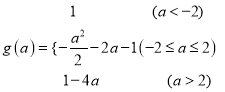题目内容
【题目】在![]() 中,
中, ![]() AD与BC交于点M,设
AD与BC交于点M,设![]() ,以
,以![]() 、
、![]() 为基底表示
为基底表示![]()

【答案】![]()
【解析】试题分析:由A、M、D三点共线,知![]() ;由C、M、B三点共线,知
;由C、M、B三点共线,知![]()
,所以 ,所以
,所以![]() =
=![]() .
.
试题解析:
设![]() ,
,
则![]()
因为A、M、D三点共线,所以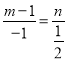 ,即
,即![]()
又![]()
因为C、M、B三点共线,所以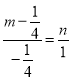 ,即
,即![]()
由![]() 解得
解得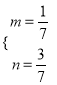 ,所以
,所以![]()
【题型】解答题
【结束】
20
【题目】函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 及此时
及此时![]() 的最大值.
的最大值.
【答案】(1) 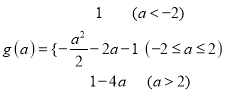 ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)利用同角三角函数间的基本关系化简函数解析式后,分三种情况:①![]() 小于﹣1时②
小于﹣1时②![]() 大于﹣1而小于1时③
大于﹣1而小于1时③![]() 大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把
大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把![]() 代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
试题解析:
(1)由![]()
![]() .这里
.这里![]()
①若![]() 则当
则当![]() 时,
时, ![]()
②若![]() 当
当![]() 时,
时, ![]()
③若![]() 则当
则当![]() 时,
时, ![]()
因此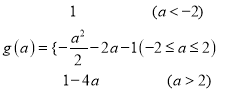
(2)![]()
![]() ①若
①若![]() ,则有
,则有![]() 得
得![]() ,矛盾;
,矛盾;
②若![]() ,则有
,则有![]() 即
即![]() 或
或![]() (舍).
(舍).
![]()
![]() 时,
时, ![]() 此时
此时![]()
当![]() 时,
时, ![]() 取得最大值为5.
取得最大值为5.

练习册系列答案
相关题目
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数).现随机抽取20天的指数(见下表),将指数不低于8.5视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
(Ⅰ)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(Ⅱ)以这20天的数据估计我市总体空气质量(天数很多).若从我市总体空气质量指数中随机抽取3天的指数,用X表示抽到空气质量为优良的天数,求X的分布列及数学期望.