Question

【题目】某企业招聘中，依次进行A科、B科考试，当A科合格时，才可考B科，且两科均有一次补考机会，两科都合格方通过．甲参加招聘，已知他每次考A科合格的概率均为 ，每次考B科合格的概率均为 ．假设他不放弃每次考试机会，且每次考试互不影响．
（I）求甲恰好3次考试通过的概率；
（II）记甲参加考试的次数为ξ，求ξ的分布列和期望．

Answer 1

【答案】解：设甲“第一次考A科成绩合格”为事件A1，“A科补考后成绩合格”为事件A2，

“第一次考B科成绩合格”为事件B1，“B科补考后成绩合格”为事件B2．

（Ⅰ）甲参加3次考试通过的概率为：

（Ⅱ）由题意知，ξ可能取得的值为：2，3，4

=

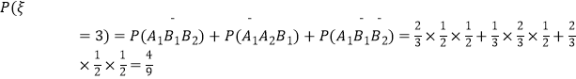
分布列（如表）

ξ	2	3	4
P

故

【解析】（I）甲参加3次考试通过分两种情况：A科考两次B科考一次和A科考一次B科考两次，分别计算每种情况的概率，进而可得甲恰好3次考试通过的概率；（II）先分别求出随机变量的所有可能取值的概率，再写出分布列，进而可得期望．
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识，掌握在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．