题目内容
抛物线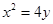
的准线方程为 ．
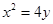的准线方程为 ．y=-1
试题分析：因为抛物线
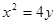的焦点在y轴上，且p=2，所以准线方程为y=-1。点评：记熟抛物线
的准线方程为
是做本题的前提条件。
练习册系列答案
相关题目
试题分析：因为抛物线
的焦点在y轴上，且p=2，所以准线方程为y=-1。点评：记熟抛物线
的准线方程为是做本题的前提条件。题目内容
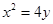的准线方程为 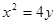．的焦点在y轴上，且p=2，所以准线方程为y=-1。的准线方程为是做本题的前提条件。
经过点
，且
是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤，可求得平面
与曲线
有两个不同的交点，则实数
的取值范围是（ ）
是椭圆
上一点，
，
是椭圆的两焦点，且满足
、
是椭圆上任两点，且直线
、
的斜率分别为
、
，若存在常数
使
，求直线
的斜率. 
两焦点为
，则椭圆上存在六个不同点
,使得
为直角三角形；
过抛物线
的焦点，且与这条抛物线交于
两点，则
的最小值为2；
的一个焦点作它的一条渐近线的垂线，垂足为
为坐标原点，则
；
⊙
则这两圆恰有2条公切线。
有共同焦点，且过点(0,2)的双曲线方程，并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
，焦点为
，顶点为
，点
在抛物线上移动，
是
的中点，
是
的中点，求点
是圆
上的动点，点D是
轴上的投影，M为
的直线被C所截线段的长度。
轴的负半轴上,过点
作直线
与抛物线交于A,B两点,且满足
,
面积的的最大值．