题目内容
已知平面 经过点
经过点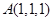 ,且
,且 是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面
是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面 的方程是 .
的方程是 .
 经过点
经过点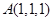 ,且
,且 是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面
是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面 的方程是 .
的方程是 .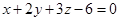
试题分析:设平面内任意一点为
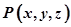
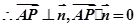 代入数据计算得平面
代入数据计算得平面 的方程为
的方程为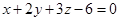
点评:本题类比平面几何求轨迹方程的方法求解

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
题目内容
 经过点
经过点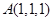 ,且
,且 是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面
是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面 的方程是 .
的方程是 .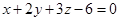
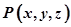
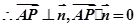 代入数据计算得平面
代入数据计算得平面 的方程为
的方程为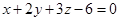

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案