题目内容
【题目】已知函数![]() .
.
(1)判断![]() 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)若![]() ,试判断函数
,试判断函数![]() 的单调性,并用定义法证明;
的单调性,并用定义法证明;
(3)若已知![]() ,且函数
,且函数![]() 在区间[1,+∞)上的最小值为-2,求实数m的值.
在区间[1,+∞)上的最小值为-2,求实数m的值.
【答案】(1)![]() 为奇函数,详见解析(2)在
为奇函数,详见解析(2)在![]() 上单调递增;证明见解析(3)
上单调递增;证明见解析(3)![]()
【解析】
(1)根据奇偶性的定义判断即可;
(2)利用定义法证明函数的单调性,按照:设元、作差、变形、判断符号、下结论的步骤完成即可;
(3)由![]() 求出
求出![]() 的值,则可得
的值,则可得![]() ,令
,令![]() ,则
,则![]() 再根据二次函数的性质计算可得;
再根据二次函数的性质计算可得;
解:(1)![]() 为奇函数
为奇函数
由题知,![]() 定义域为
定义域为![]() ,又
,又![]()
因此![]() 为奇函数
为奇函数
(2)![]() ,
,![]() 在
在![]() 上单调递增
上单调递增
证明如下:
任取![]() 且
且![]() ,则
,则
 .
.
∵![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 即
即![]() .
.
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
(3)![]() ,由
,由![]() 得
得![]() ,
,
解得![]() 或
或![]() ,∵
,∵![]() 且
且![]() ,∴
,∴![]() ,
,![]() ,
,
![]()
令![]() ,∵
,∵![]() ,
,![]() 在定义域上单调递增,
在定义域上单调递增,![]() 在定义域上单调递减,故
在定义域上单调递减,故![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,
,
则![]() ,
,
①当![]() 时,
时,![]() 时有,
时有,![]() 解得
解得![]() 符合题意;
符合题意;
②当![]() 时,
时,![]() 时有
时有![]() ,解得
,解得![]() ,不成立舍去.
,不成立舍去.
综上所述![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了了解某市民众对某项公共政策的态度,在该市随机抽取了50名市民进行调查,作出他们的月收入(单位:百元,范围:![]() )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:

月收入 | 赞成的人数 |
| 4 |
| 8 |
| 12 |
| 5 |
| 2 |
| 2 |
(1)求月收入在![]() 内的频率,补全频率分布直方图,并在图中标出相应纵坐标;
内的频率,补全频率分布直方图,并在图中标出相应纵坐标;
(2)若从月收入在![]() 内的被调查者中随机选取2人,求这2人对该项政策都不赞成的概率.
内的被调查者中随机选取2人,求这2人对该项政策都不赞成的概率.
【题目】已知函数y=a+bx与![]() ,若对于任意一点
,若对于任意一点![]() ,过点
,过点![]() 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() ,定义:
,定义:![]() ,若
,若![]() 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数![]() 来拟合Y与X之间的关系
来拟合Y与X之间的关系
(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数![]() 与函数
与函数![]() ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
(2)若一组变量的散点图符合![]() 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当![]() 时,
时,![]() 的值为多少.
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:对于一组数据![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为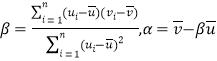 )
)