题目内容
曲线y="sinx+e" x在点(0,1)处的切线方程是( )
| A.x-3y+3=0 | B.x-2y+2=0 |
| C.2x-y+1="0" | D.3x-y+1=0 |
C
解:∵f(x)=ex+sinx=
∴f′(x)=ex+cosx,∴在x=0处的切线斜率k=f′(0)=1+1=2,
∴f(0)=1+0=1,
∴f(x)=ex+sinx在x=0处的切线方程为:y-1=2x,
∴y=2x+1,
故答案为:y=2x+1
∴f′(x)=ex+cosx,∴在x=0处的切线斜率k=f′(0)=1+1=2,
∴f(0)=1+0=1,
∴f(x)=ex+sinx在x=0处的切线方程为:y-1=2x,
∴y=2x+1,
故答案为:y=2x+1

练习册系列答案
相关题目
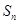 与n之间的关系如图所示,从目前记录的结果看,前m年的年平均产量最高,m的值为( )
与n之间的关系如图所示,从目前记录的结果看,前m年的年平均产量最高,m的值为( )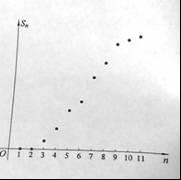
 与
与 ,
,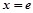 及
及 轴围成图形的面积是( )
轴围成图形的面积是( )

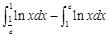

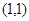 处的切线方程为________
处的切线方程为________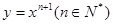 在点(1,1)处的切线与
在点(1,1)处的切线与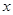 轴的交点的横坐标为
轴的交点的横坐标为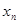 ,令
,令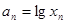 ,则
,则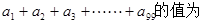 ______________
______________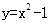 ,直线
,直线 和
和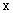 轴围城的封闭图形(阴影)的面积为( )
轴围城的封闭图形(阴影)的面积为( )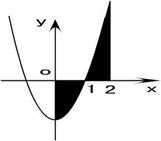
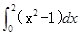
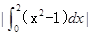
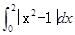
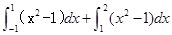
 ,则
,则 ( )
( )



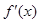 ,且满足f(x)= x3+2x
,且满足f(x)= x3+2x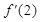 ,则
,则