题目内容
15.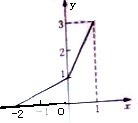 函数f(x)的图象是由两条线段组成的折线段(如图所示),则函数f(x)的表达式为f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.
函数f(x)的图象是由两条线段组成的折线段(如图所示),则函数f(x)的表达式为f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.
分析 分段求出函数的解析式,即可得出结论.
解答 解:当-2≤x≤0时,直线的方程为$\frac{x}{-2}+y=1$,即y=$\frac{1}{2}$x+1;
0≤x≤1时,设直线的方程为y=kx+b,代入(0,1),(1,3),可得$\left\{\begin{array}{l}{b=1}\\{k+b=3}\end{array}\right.$,
∴k=2,b=1,∴y=2x+1,
∴f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.
故答案为:f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.
点评 本题考查函数的解析式,考查学生的计算能力,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
5.如果一条直线与一个平面平行,则这条直线与这个平面内直线的位置关系为( )
| A. | 平行或相交 | B. | 平行或异面 | C. | 相交或异面 | D. | 都有可能 |
6.若一个底面是正三角形的三棱柱的正视图如图所示,则其体积等于( )
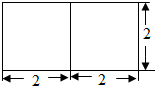

| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |