题目内容
7．若x∈[4，+∞），求函数y=$\frac{{x}^{2}-2x+3}{x+1}$的值域．分析 化简：y=$\frac{{x}^{2}-2x+3}{x+1}$=$\frac{（x+1）^{2}-4x+2}{x+1}$=x+1+$\frac{6}{x+1}$-4，从而可得y=$\frac{{x}^{2}-2x+3}{x+1}$在[4，+∞）上是增函数，从而解得．
解答 解：y=$\frac{{x}^{2}-2x+3}{x+1}$=$\frac{（x+1）^{2}-4x+2}{x+1}$=x+1+$\frac{6}{x+1}$-4，
∵x+1+$\frac{6}{x+1}$≥2$\sqrt{6}$，（当且仅当x+1=$\frac{6}{x+1}$，即x=$\sqrt{6}$-1时，等号成立），
又∵x∈[4，+∞），
∴$\sqrt{6}$-1取不到，
可判断y=$\frac{{x}^{2}-2x+3}{x+1}$在[4，+∞）上是增函数，
故y≥$\frac{16-8+3}{5}$=$\frac{11}{5}$，
故函数y=$\frac{{x}^{2}-2x+3}{x+1}$的值域为[$\frac{11}{5}$，+∞）．
点评 本题考查了函数的单调性的判断及对勾函数的应用，同时考查了函数的值域的求法．
练习册系列答案
名校课堂系列答案
相关题目
17．正弦定理的内容是（ ）
| A． | $\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$ | B． | $\frac{a}{cosA}=\frac{b}{cosB}=\frac{c}{cosC}$ | ||
| C． | $\frac{a}{sinA}=\frac{b}{cosB}=\frac{c}{tanC}$ | D． | 以上结果都不正确 |
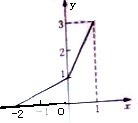函数f（x）的图象是由两条线段组成的折线段（如图所示），则函数f（x）的表达式为f（x）=$\left\{\begin{array}{l}{\frac{1}{2}x+1，-2≤x≤0}\\{2x+1，0≤x≤1}\end{array}\right.$．