题目内容
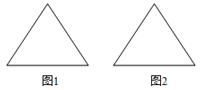
【题目】给出两块面积相同的正三角形纸片如图，要求用其中一块剪拼成一个正三棱锥（正三棱锥的三个侧面是全等的等腰三角形）模型，另一块剪拼成一个正三棱柱（正三棱柱上、下底面是正三角形，侧面是矩形）模型，使纸片正好用完，请设计一种剪拼方法，分别标示在图（1）（2）中，并作简要说明.
【答案】详见解析
【解析】
从正三棱锥和正三棱柱的主要特征入手进行设计，比如底面是正三角形等.
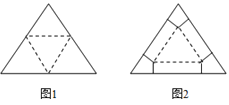
如图（1），沿正三角形三边中点连线折起，可拼得一个正三棱锥.
如图（2），从正三角形三个角上分别剪去三个相同的四边形，其较长的一组邻边边长为原三角形边长的
，有一组对角为直角，余下部分按虚线折起，可拼得一个缺上底的正三棱柱，而剪去的三个相同的四边形恰好可拼成这个正三棱柱的上底.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】某地随着经济的发展，居民收入逐年增长，下表是该地一建设银行连续五年的储蓄存款（年底余额），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便，工作人员将上表的数据进行了处理， 
得到下表2：
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求z关于t的线性回归方程；
（Ⅱ）通过（Ⅰ）中的方程，求出y关于x的回归方程；
（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
（附：对于线性回归方程
，其中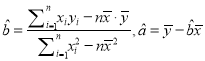
）
