题目内容
【题目】已知椭圆![]() ,四点
,四点 ,
,![]() ,
, ,
, 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之积为定值?若存在,求出点
的斜率之积为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,点
;(2)存在,点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)根据椭圆的对称性可知点![]() 、
、![]() 、
、![]() 在椭圆
在椭圆![]() 上,可得出关于
上,可得出关于![]() 、
、![]() 的方程组,解出
的方程组,解出![]() 和
和![]() 的值,即可求得椭圆
的值,即可求得椭圆![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,结合斜率公式并代入韦达定理,由已知条件可求得实数
的方程联立,列出韦达定理,结合斜率公式并代入韦达定理,由已知条件可求得实数![]() 的值,进而得解.
的值,进而得解.
(1)由于![]() 、
、![]() 两点关于
两点关于![]() 轴对称,故由题设知
轴对称,故由题设知![]() 经过
经过![]() 、
、![]() 两点
两点
易知椭圆![]() 不经过点
不经过点![]() ,所以点
,所以点![]() 在
在![]() 上,因此
上,因此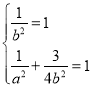 ,解得
,解得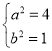 ,
,
因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)由题意知直线![]() 的斜率不为
的斜率不为![]() ,
,
设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() ,
,![]() ,
,![]() ,
,
设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
由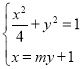 ,消去
,消去![]() ,得
,得![]() ,
,
易知![]() ,得
,得![]() ,
,![]() ,
,
![]()
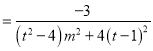 .
.
当![]() ,即
,即![]() 时,
时,![]() 为定值,
为定值,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
此时点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目
【题目】A药店计划从甲,乙两家药厂选择一家购买100件某种中药材,为此A药店从这两家药厂提供的100件该种中药材中随机各抽取10件,以抽取的10件中药材的质量(单位:克》作为样本.样本数据的茎叶图如图所示.己知A药店根据中药材的质量(单位:克)的往定性选择药厂

(1)根据样本数据,A药店应选择哪家药厂购买中药材?
(2)若将抽取的样本分布近似看作总体分布,药店与所选药厂商定中药材的购买价格如下表:
每件中药材的质量(单位:克) | 购买价格(单位:元/件) |
|
|
|
|
|
|
(i)估计![]() 药店所购买的
药店所购买的![]() 件中药材的总质量;
件中药材的总质量;
(ii)若![]() 药店所购买的
药店所购买的![]() 件中药材的总费用不超过
件中药材的总费用不超过![]() 元.求
元.求![]() 的最大值.
的最大值.