题目内容
8.已知$\overrightarrow{AB}⊥\overrightarrow{AC},|{\overrightarrow{AB}}|=\frac{1}{t},|{\overrightarrow{AC}}|=t$,若P点是△ABC所在平面内一点,且$\overrightarrow{AP}=\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|}}+\frac{{4\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|}}$,则$\overrightarrow{PB}•\overrightarrow{PC}$的最大值等于( )| A. | 13 | B. | 15 | C. | 19 | D. | 21 |
分析 建系,由向量式的几何意义易得P的坐标,可化$\overrightarrow{PB}•\overrightarrow{PC}$=-4($\frac{1}{t}$-4)-(t-1)=17-(4•$\frac{1}{t}$+t),由基本不等式可得.
解答 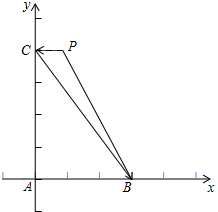 解:由题意建立如图所示的坐标系,
解:由题意建立如图所示的坐标系,
可得A(0,0),B($\frac{1}{t}$,0),C(0,t),
∵$\overrightarrow{AP}=\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|}}+\frac{{4\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|}}$,∴P(1,4),
∴$\overrightarrow{PB}$=($\frac{1}{t}$-1,-4),$\overrightarrow{PC}$=(-1,t-4),
∴$\overrightarrow{PB}•\overrightarrow{PC}$=-4($\frac{1}{t}$-4)-(t-1)=17-(4t+$\frac{1}{t}$),
由基本不等式可得$\frac{1}{t}$+4t≥2$\sqrt{\frac{1}{t}•4t}$=4,
∴17-(4t+$\frac{1}{t}$)≤17-4=13,
当且仅当4t=$\frac{1}{t}$即t=$\frac{1}{2}$时取等号,
∴$\overrightarrow{PB}•\overrightarrow{PC}$的最大值为13,
故选:A.
点评 本题考查平面向量数量积的运算,涉及基本不等式求最值,属中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
18.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}+2π$ | B. | $\frac{13π}{6}$ | C. | $\frac{7π}{3}$ | D. | $\frac{5π}{2}$ |
19.若(1+i)+(2-3i)=a+bi(a,b∈R,i是虚数单位),则a,b的值分别等于( )
| A. | 3,-2 | B. | 3,2 | C. | 3,-3 | D. | -1,4 |
3.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程$\hat y=\hat bx+\hat a$,其中$\hat b=0.76,\hat a=\overline y-\hat b\overline x$,据此估计,该社区一户收入为15万元家庭年支出为( )
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.4万元 | B. | 11.8万元 | C. | 12.0万元 | D. | 12.2万元 |
 已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,
已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,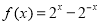 ,数列
,数列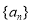 满足
满足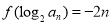 .
.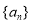 的通项公式;
的通项公式;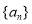 是递减数列.
是递减数列.