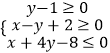题目内容
【题目】已知圆C：（x+2）2+y2=5，直线l：mx﹣y+1+2m=0，m∈R．
（1）求证：对m∈R，直线l与圆C总有两个不同的交点A、B；
（2）求弦AB的中点M的轨迹方程，并说明其轨迹是什么曲线；
（3）是否存在实数m，使得圆C上有四点到直线l的距离为 
？若存在，求出m的范围；若不存在，说明理由．
【答案】
（1）解：圆C：（x+2）2+y2=5，的圆心为C（﹣2，0），半径为 
，所以圆心C到直线l：mx﹣y+1+2m=0的距离 
．
所以直线l与圆C相交，即直线l与圆C总有两个不同的交点；
（2）解：设中点为M（x，y），因为直线l：mx﹣y+1+2m=0恒过定点（﹣2，1），
当直线l的斜率存在时， 
，又 
，kABkMC=﹣1，
所以 
，化简得 
．
当直线l的斜率不存在时，中点M（﹣2，0）也满足上述方程．
所以M的轨迹方程是 
，它是一个以 
为圆心，以 
为半径的圆．
（3）解：假设存在直线l，使得圆上有四点到直线l的距离为 
，由于圆心C（﹣2，0），半径为 ，则圆心C（﹣2，0）到直线l的距离为 
化简得m2＞4，解得m＞2或m＜﹣2．
【解析】（1）根据点到直线的公式，不难判断出圆心到动直线的距离小于半径R，故结论得证，（2）设动点M的坐标为（x，y），由于直线l恒过定点，分类讨论当直线斜率存在和斜率不存在，圆心与M点所在直线与直线AB互相垂直，故可以列出关系式，从而得到轨迹方程，（3）假设存在直线l使得条件成立，表示出圆心到直线l的距离小于半径减去，解出m的范围即可.
【考点精析】利用直线与圆的三种位置关系对题目进行判断即可得到答案，需要熟知直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点．
