题目内容
【题目】设f(x)是定义在[﹣1,1]上的奇函数,f(﹣1)=﹣1,且对任意a,b∈[﹣1,1],当a≠b时,都有 ![]() ;
;
(1)解不等式f ![]() ;
;
(2)若f(x)≤m2﹣2km+1对所有x∈[﹣1,1],k∈[﹣1,1]恒成立,求实数m的取值范围.
【答案】
(1)解:∵f(x)是定义在[﹣1,1]上的奇函数,
且对任意a,b∈[﹣1,1],当a≠b时,都有 ![]() ,
,
∴函数f(x)在区间[﹣1,1]上单调递增,
又f ![]() ,
,
∴ 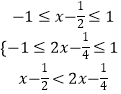 ,解得:﹣
,解得:﹣ ![]() <x≤
<x≤ ![]() ,
,
∴不等式f ![]() 的解集为{x|﹣
的解集为{x|﹣ ![]() <x≤
<x≤ ![]() }
}
(2)解:∵奇函数f(x)在区间[﹣1,1]上单调递增,且f(﹣1)=﹣1,
∴f(x)max=f(1)=﹣f(﹣1)=1,
故f(x)≤m2﹣2km+1对所有x∈[﹣1,1],k∈[﹣1,1]恒成立m2﹣2km+1≥f(x)max=1,
∴m2﹣2km≥0恒成立(﹣1≤k≤1),
令g(k)=﹣2mk+m2,
则 ![]() ,即
,即 ![]() ,解得:m≥2或m≤﹣2或m=0.
,解得:m≥2或m≤﹣2或m=0.
∴实数m的取值范围为(﹣∞,﹣2]∪[2,+∞)∪{0}
【解析】(1)f(x)在[﹣1,1]上是增函数,然后利用增函数的定义进行证明,将不等式结合函数的单调性进行转化,解得答案,(2)根据函数的单调性知f(x)最大值为f(1)=1,所以要使f(x)≤m2﹣2km+1对所有x∈[﹣1,1],k∈[﹣1,1]恒成立,只需要m2﹣2km≥0恒成立(﹣1≤k≤1),进而得到实数m的取值范围.
【考点精析】通过灵活运用函数奇偶性的性质,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案