Question

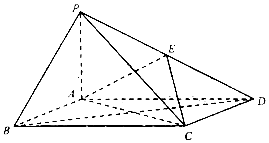
【题目】如图所示，MCN是某海湾旅游区的一角，为营造更加优美的旅游环境，旅游区管委会决定建立面积为4 平方千米的三角形主题游戏乐园ABC，并在区域CDE建立水上餐厅．已知∠ACB=120°，∠DCE=30°．
（1）设AC=x，AB=y，用x表示y，并求y的最小值；
（2）设∠ACD=θ（θ为锐角），当AB最小时，用θ表示区域CDE的面积S，并求S的最小值．

Answer 1

【答案】
（1）解：∵AC=x，AB=y，∠ACB=120°，

S△ABC= ACBCsin120°= =4 ，

∴BC= ．

△ABC中，利用余弦定理可得AB2=AC2+BC2﹣2ACBCcos120°，

即y2=x2+ +16≥2 +16=48，

∴y≥4 ，当且仅当x2=16，即x=4时，取等号，

故当x=4时，y取得最小值为4 ．

（2）解：设∠ACD=θ（θ为锐角），

当AB最小时，x=AC=4=BC，AB=4 ，∠CAB=∠CBA=30°，

△ACD中，由正弦定理可得 = ，

∴CD= = = ，

△ACE中，由正弦定理可得CE= = = ，

根据区域CDE的面积S= CDCEsin30°= = ，

故当2θ= ，即θ= 时，区域CDE的面积S取得最小值为 =8﹣4 ．

【解析】1、根据题意可设AC=x，AB=y利用余弦定理求得BC的值即得y的函数解析式再利用基本不等式求得y的最小值。
2、由题意可知在△ACD中根据正弦定理求得CD的值在△ACE中再根据正弦定理求得CE的值。根据区域CDE的面积S=,利用正弦函数的值域求得区域CDE的面积最小值。