题目内容
【题目】已知圆心在
轴非负半轴上，半径为2的圆C与直线
相切.
(1)求圆C的方程；
(2)设不过原点O的直线l与圆O:x2+y2=4相交于不同的两点A，B.①求△OAB的面积的最大值;②在圆C上，是否存在点M(m，n)，使得直线l的方程为mx+ny=1，且此时△OAB的面积恰好取到①中的最大值?若存在，求出点M的坐标；若不存在，请说明理由.
【答案】（1）
；（2）① 2 ② 
.
【解析】
(1)设出圆心坐标，根据点到直线距离求得圆心，进而得到圆的方程。
(2)设圆心到直线AB的距离，根据三角形面积公式和基本不等式即可求得面积的最大值；根据点M在圆上，及点到直线距离等于半径即可求得M的坐标。
(1)设圆心是(x0，0)(
)，它到直线
的距离是
解得
或
(舍去)
∴所求圆C的方程是
.
(2)①设圆心O到直线
的距离为
则△OAB的面积
当且仅当
时等号成立
∴△OAB的最大面积为2.
②由题得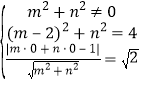
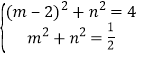即
即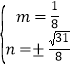
∴存在满足要求的点M，其坐标是,
练习册系列答案
相关题目
【题目】学校某文具商店经营某种文具，商店每销售一件该文具可获利3元，若供大于求则削价处理，每处理一件文具亏损1元；若供不应求，则可以从外部调剂供应，此时每件文具仅获利2元．为了了解市场需求的情况，经销商统计了去年一年（52周）的销售情况．
销售量（件） | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
以去年每周的销售量的频率为今年每周市场需求量的概率．
（1）要使进货量不超过市场需求量的概率大于0.5，问进货量的最大值是多少？
（2）如果今年的周进货量为14，写出周利润Y的分布列；
（3）如果以周利润的期望值为考虑问题的依据，今年的周进货量定为多少合适？
