Question

【题目】已知函数f（x）=cos（x+ ）+sinx．
（I）利用“五点法”，列表并画出f（x）在[﹣ ， ]上的图象；
（II）a，b，c分别是△ABC中角A，B，C的对边．若a= ，f（A）= ，b=1，求△ABC的面积．

x
f（x）

Answer 1

【答案】解：（Ⅰ）f（x）=cos（x+ ）+sinx=cosxcos ﹣sinxsin +sinx
= cosx+ sinx
=sin（x+ ），
利用“五点法”列表如下，

x+	0		π		2π
x	﹣
y	0	1	0	﹣1	0

画出f（x）在[﹣ ， ]上的图象，如图所示：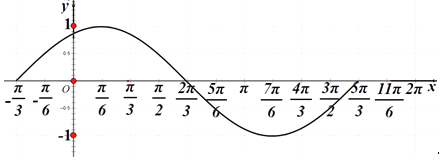

（Ⅱ）由（Ⅰ）f（A）=sin（A+ ）= ，在△ABC中，0＜A＜π，可知A= ．
由正弦定理可知 ，即 ，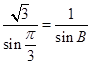
所以sinB= ，
又0 ，
∴B= ，
∴C= ，
∴S= ab= = ．
因此△ABC面积是 ．
【解析】（Ⅰ）利用三角函数恒等变换的应用化简函数解析式可得f（x）=sin（x+ ），利用“五点法”，即可列表并画出函数的图象．（Ⅱ）由（Ⅰ）可得sin（A+ ）= ，结合范围0＜A＜π，可求A，由正弦定理可求sinB= ，结合范围0 ，可求B，进而可求C，利用三角形面积公式即可计算得解．
【考点精析】本题主要考查了五点法作函数y=Asin（ωx+φ）的图象的相关知识点，需要掌握描点法及其特例—五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）才能正确解答此题．