题目内容
【题目】如图，双曲线的中心在坐标原点O，M、N分别为双曲线虚轴的上、下端点，A是双曲线的右顶点，F是双曲线的右焦点，直线AM与FN相交于点P，若∠APF是锐角，则此双曲线的离心率的取值范围是（ ）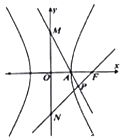 
A.（ 
，+∞）
B.（1+ 
，+∞）
C.（0， 
）
D.（ 
，+∞）
【答案】A
【解析】解：设双曲线的方程为 
=1， 由题意可得A（a，0），F（c，0），M（0，b），N（0，﹣b），
故直线AF的方程为y+b= 
x，直线NF的方程为y﹣b=﹣ 
x，
联立方程组，解得x= 
，y= 
，
即P（ ， ），
∴ 
=（ 
， ）， 
=（ 
， ），
∵∠APF是锐角，
∴ 
= + ＜0，
∴b2＜ac，
∴c2﹣a2＜ac
∴e﹣ 
＜1，
即e2﹣e﹣1＜0，
解得e＞ 
，e＜ 
（舍去），
故选：A
【题目】近年来，手机已经成为人们日常生活中不可缺少的产品，手机的功能也日趋完善，已延伸到了各个领域，如拍照，聊天，阅读，缴费，购物，理财，娱乐，办公等等，手机的价格差距也很大，为分析人们购买手机的消费情况，现对某小区随机抽取了200人进行手机价格的调查，统计如下：
年龄 价格 | 5000元及以上 | 3000元﹣4999元 | 1000元﹣2999元 | 1000元以下 |
45岁及以下 | 12 | 28 | 66 | 4 |
45岁以上 | 3 | 17 | 46 | 24 |
（Ⅰ）完成关于人们使用手机的价格和年龄的2×2列联表，再判断能否在犯错误的概率不超过0.025的前提下，认为人们使用手机的价格和年龄有关？
（Ⅱ）从样本中手机价格在5000元及以上的人群中选择3人调查其收入状况，设3人中年龄在45岁及以下的人数为随机变量X，求随机变量X的分布列及数学期望．
附K2= 
P（K2≥k） | 0.05 | 0.025 | 0.010 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】2016年微信用户数量统计显示，微信注册用户数量已经突破9.27亿．微信用户平均年龄只有26岁，97.7%的用户在50岁以下，86.2%的用户在18﹣36岁之间．为调查大学生这个微信用户群体中每人拥有微信群的数量，现从北京市大学生中随机抽取100位同学进行了抽样调查，结果如下：
微信群数量 | 频数 | 频率 |
0至5个 | 0 | 0 |
6至10个 | 30 | 0.3 |
11至15个 | 30 | 0.3 |
16至20个 | a | c |
20个以上 | 5 | b |
合计 | 100 | 1 |
（Ⅰ）求a，b，c的值；
（Ⅱ）若从这100位同学中随机抽取2人，求这2人中恰有1人微信群个数超过15个的概率；
（Ⅲ）以这100个人的样本数据估计北京市的总体数据且以频率估计概率，若从全市大学生中随机抽取3人，记X表示抽到的是微信群个数超过15个的人数，求X的分布列和数学期望EX．
