题目内容
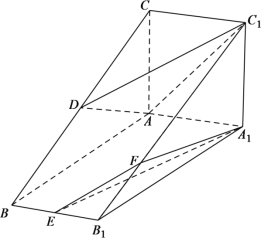
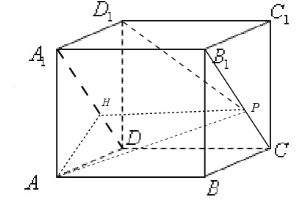
【题目】已知:在长方体![]() 中,
中,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,则①
上的一个动点,则①![]() 的最小值等于__________;②直线
的最小值等于__________;②直线![]() 与平面
与平面![]() 所成角的正切值的取值范围为____________.
所成角的正切值的取值范围为____________.
【答案】![]()
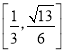
【解析】
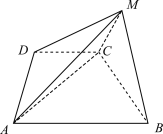
①将△AB1C与△D1B1C以公共边B1C为邻边展开成一个平行四边形,其对角线AD1的长度即为所求.
②P点在B1C上移动,它在平面ADD1上的射影H落在A1D上,此时PH是定值A1B1,只需研究AH的范围即可.
长方体中,∵AB=1,AD=2,AA1=3,点P是线段B1C上的一个动点.
①由长方体的性质可知,![]() ,
,![]() ,
,![]() .
.
将△AB1C与△D1CB1以B1C为公共边展开成一平面四边形AB1D1C,如图:
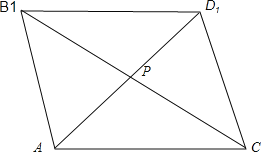
易证四边形AB1D1C是平行四边形,所以当APD1三点共线时,即AP+D1P=AD1时最小.
根据平行四边形对角线和四条边的性质即:![]() ,
,
代入数据得:![]() ,解得
,解得![]() .
.
∴AP+D1P的最小值等于![]() .
.
②由长方体的性质可知,对角面A1B1CD⊥平面ADD1A1,交线为A1D.
所以由点P向直线A1D作垂线PH,则PH⊥平面ADD1A1.
连接AH,则∠PAH即为直线PA与平面AA1D1D所成角.
显然PH=AB=1为定值.
设Rt△A1AD斜边上的高为h,则A1Dh=ADAA1,求得h![]() ,此时AH最短.
,此时AH最短.
结合A1A=3,所以![]() ,
,
所以tan∠PAH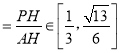 .
.
故答案为:![]() ,
,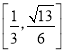 .
.

练习册系列答案
相关题目