题目内容
【题目】已知双曲线
的右焦点为点
，点
是虚轴的一个端点，点
为双曲线
左支上的一个动点，则
周长的最小值等于____________.
【答案】4
【解析】
先由双曲线的几何性质写出B和F的坐标，并求得|BF|的长，然后设双曲线的左焦点为E，由双曲线的定义可知，|PF|﹣|PE|＝2a，而△BPF的周长为|BF|+|PF|+|PB|＝|BF|+2a+（|PE|+|PB|），求出|PE|+|PB|的最小值即可得△BPF周长的最小值，当且仅当B、P、E三点共线时，可得解．
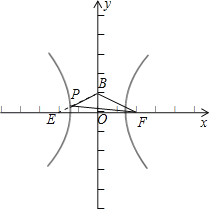
∵双曲线
，∴F
，
如图所示，不妨设B为x轴上方的虚轴端点，则B（0，1），|BF|＝2，
设双曲线的左焦点为E，由双曲线的定义可知，|PF|﹣|PE|＝2a
，即|PF|＝|PE|，
∴△BPF的周长为|BF|+|PF|+|PB|＝|BF|+（|PE|）+|PB|＝2
|PE|+|PB|≥2|BE|＝4，
当且仅当B、P、E三点共线时，等号成立．
所以△BPF周长的最小值等于4．
故答案为：4．
练习册系列答案
应用题作业本系列答案
相关题目
