题目内容
18.已知(1-2x)7=a0+a1x+a2x2+…+a7x7,求:(1)求展开式中的常数项;
(2)求含x3项的系数;
(3)求a1+a2+…+a7的值.
分析 本题由于是求二项式展开式的系数之和,故可以令二项式中的x=1,又由于所求之和不含a0,令x=0,可求出a0的值,代入即求答案
解答 解:因为展开式的通项为${T}_{r+1}={C}_{7}^{r}(-2)^{r}{x}^{r}$,
所以(1)展开式的常数项为r=0时a0=1;
(2)令r=3,得到含x3项为${T}_{4}={C}_{7}^{3}(-2)^{3}{x}^{3}$=-280x3,所以含x3项的系数是-280;
(3)令x=1代入二项式(1-2x)7=a0+a1x+a2x2+…+a7x7得,(1-2)7=a0+a1+…+a7=-1,
令x=0得a0=1
∴1+a1+a2+…+a7=-1
∴a1+a2+…+a7=-2.
点评 本题主要考查二项式定理的应用;求特征项要明确通项;一般在求解有二项式的系数的和等问题时,通常会将二项式展开式中的未知数x赋值为1或0或者是-1进行求解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8.程序框图的基本要素为输入、输出、条件和( )
| A. | 判断 | B. | 有向线 | C. | 循环 | D. | 开始 |
6.已知条件p:|5x-2|>3,q:$\frac{1}{{x}^{2}+4x-5}>0$,则“¬p”是“¬q”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.已知y=ksinx+1,x∈R,则y的最大值为$\left\{\begin{array}{l}{k+1,k>0}\\{1,k=0}\\{-k+1,k<0}\end{array}\right.$.
7.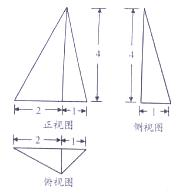 若某几何体的三视图如图所示,则该几何体的体积为( )
若某几何体的三视图如图所示,则该几何体的体积为( )
 若某几何体的三视图如图所示,则该几何体的体积为( )
若某几何体的三视图如图所示,则该几何体的体积为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | 2 | D. | 6 |