题目内容
9.已知圆C1:x2+y2+2x+2y-8=0与圆C2:x2+y2-2x+10y-24=0相交于AB两点,则公共弦AB所在直线方程为x-2y+4=0.分析 写出过两个圆的圆系方程,令λ=-1即可求出公共弦所在直线方程.
解答 解:(1)经过圆C1:x2+y2+2x+2y-8=0与圆C2:x2+y2-2x+10y-24=0的公共点的圆系方程为:
x2+y2+2x+2y-8+λ(x2+y2-2x+10y-24)=0,
令λ=-1,可得公共弦所在直线方程:x-2y+4=0.
故答案为:x-2y+4=0.
点评 本题是基础题,考查圆系方程的有关知识,公共弦所在直线方程,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在某项测量中,测量结果X服从正态分布N(2,σ2),若X在(0,4)内取值的概率为0.6,则X在(0,2)内取值的概率为( )
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.6 |
1.已知命题P:?x0∈R,tanx0≥1,则它的否定为( )
| A. | ?x∈R,tanx≥1 | B. | ?x0∈R,tanx0>1 | C. | ?x∈R,tanx<1 | D. | ?x0∈R,tanx0<1 |
19.在极坐标系中,直线ρcosθ=1与圆ρ=2cosθ的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交但不过圆心 | D. | 相交且过圆心 |
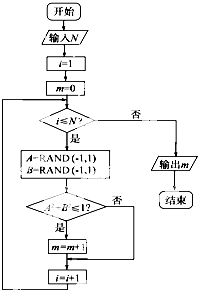 如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产
如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产