题目内容
20.函数f(x)=x3ex的极值点x0=-3,曲线y=f(x)在点(x0,f(x0))处的切线方程是y=-27e-3.分析 先求出函数f(x)的导数,令导函数等于0,求出x0,从而求出切线方程.
解答 解:f′(x)=3x2•ex+x3ex=x2ex(x+3),
令f′(x)=0,解得:x=-3,
∴x0=-3,f(x0)=-27e-3,
∴切线方程是:y=-27e-3,
故答案为:-3,y=-27e-3
点评 本题考查了导数的应用,考查函数的切线方程,是一道基础题.

练习册系列答案
相关题目
10.命题“?x0∈R,2${\;}^{{x}_{0}}$≥1”的否定是( )
| A. | ?x0∈R,2${\;}^{{x}_{0}}$<1 | B. | ?x0∈R,2${\;}^{{x}_{0}}$≤1 | C. | ?x∈R,2x≥1 | D. | ?x∈R,x<1 |
11.某校高一年段为了控制学生迟到现象,特别规定在每周周一到周五这五天中,“连续5天,每天迟到都不超过5人次的班级才有资格争夺年段流动红旗”.根据过去5天年段统计的一到四班迟到学生人此数据的数字特征,一定有资格的是( )
| A. | 一班:总体均值为2,总体方差为2 | B. | 二班:总体均值为3,中位数为3 | ||
| C. | 三班:总体均值为2,总体方差大于0 | D. | 四班:中位数为2,众数为2 |
15.已知点A(a,a)(a≠0),B(1,0),O为坐标原点.若点C在直线OA上,且BC与OA垂直,则点C的坐标是( )
| A. | $(\frac{1}{2},\;-\frac{1}{2})$ | B. | $(\frac{a}{2},\;-\frac{a}{2})$ | C. | $(\frac{a}{2},\;\frac{a}{2})$ | D. | $(\frac{1}{2},\;\frac{1}{2})$ |
5.sin$\frac{20π}{3}$的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
9.已知数列{an}为等差数列,其公差为-2,且a5是a2与a7的等比中项,Sn为{an}(n∈N*)的前n项和,则S8的值为( )
| A. | -104 | B. | -108 | C. | 108 | D. | 104 |
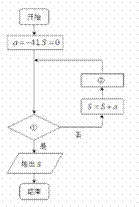 右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.
右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.