题目内容
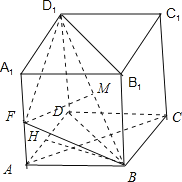
【题目】如图,已知在棱柱![]() 的面底是菱形,且
的面底是菱形,且![]() 面ABCD,
面ABCD,
![]() 为棱
为棱![]() 的中点,M为线段
的中点,M为线段![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.

【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)因为底面是菱形,所以AC⊥面BDD1B,又MF∥AC,所以MF⊥面BDD1B,即平面![]() 平面
平面![]() ;(2)过点B作BH⊥AD于H,可证出BH⊥平面ADD1A1,从而BH是三棱锥B﹣DD1F的高,求出△DD1F的面积,计算出三棱锥D1﹣BDF的体积.
;(2)过点B作BH⊥AD于H,可证出BH⊥平面ADD1A1,从而BH是三棱锥B﹣DD1F的高,求出△DD1F的面积,计算出三棱锥D1﹣BDF的体积.
试题解析:
(1)证明:∵底面是菱形,
∴AC⊥BD;
又∵B1B⊥面ABCD,AC面ABCD
∴AC⊥B1B,BD∩B1B=B,
∴AC⊥面BDD1B1
又∵MF∥AC,
∴MF⊥面BDD1B1;
又∵MF平面D1FB,
∴平面D1FB⊥平面BDD1B1;
(2)如图,过点B作BH⊥AD,垂足为H,
∵AA1⊥平面ABCD,BH平面ABCD,
∴BH⊥AA1,
∵AD、AA1是平面ADD1A1内的相交直线,
∴BH⊥平面ADD1A1,
在Rt△ABH中,∠DAB=60°,AB=AD=1,
∴BH=ABsin60°=![]() ,
,
∴三棱锥D1﹣BDF的体积为
V=![]() =
=![]() ×S△DD1FBH=
×S△DD1FBH=![]() ×
×![]() ×1×1×
×1×1×![]() =
=![]() .
.

【题目】某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: 
分数段(分) | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] | 合计 |
频数 | b | |||||
频率 | a | 0.25 |
(1)表中a,b的值及分数在[90,100)范围内的学生,并估计这次考试全校学生数学成绩及格率(分数在[90,150]范围为及格);
(2)从大于等于110分的学生随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.