题目内容
【题目】解答
(1)已知2sinx=sin( ![]() ﹣x),求
﹣x),求 ![]() 的值;
的值;
(2)求函数f(x)=ln(sinx﹣ ![]() )+
)+ ![]() 的定义域.
的定义域.
【答案】
(1)解:∵2sinx=sin( ![]() ﹣x)=cosx,
﹣x)=cosx,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
(2)解:要使函数有意义,则  ,即
,即 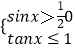 ,
,
即  ,
,
即2kπ+ ![]() <x≤2kπ+
<x≤2kπ+ ![]() ,或2kπ+
,或2kπ+ ![]() <x<2kπ+
<x<2kπ+ ![]() ,k∈Z,
,k∈Z,
即函数的定义域为(2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ]∪(2kπ+
]∪(2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ),k∈Z
),k∈Z
【解析】(1)根据条件得到cosx=2sinx,利用1的代换进行化简即可.(2)根据函数成立的条件即可求函数的定义域.
【考点精析】利用函数的定义域及其求法和函数的值域对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.

【题目】为调查某地人群年龄与高血压的关系,用简单随机抽样方法从该地区年龄在20~60岁的人群中抽取200人测量血压,结果如下:
高血压 | 非高血压 | 总计 | |
年龄20到39岁 | 12 |
| 100 |
年龄40到60岁 |
| 52 | 100 |
总计 | 60 |
| 200 |
(1)计算表中的![]() 、
、![]() 、
、![]() 值;是否有99%的把握认为高血压与年龄有关?并说明理由.
值;是否有99%的把握认为高血压与年龄有关?并说明理由.
(2)现从这60名高血压患者中按年龄采用分层抽样的方法抽取5人,再从这5人中随机抽取2人,求恰好一名患者年龄在20到39岁的概率.
附参考公式及参考数据: ![]() =
=![]()
P(k2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |


