题目内容
设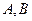 分别为椭圆
分别为椭圆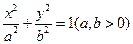 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且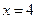 为它的右准线.
为它的右准线.
(Ⅰ)求椭圆的方程;
(Ⅱ)设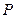 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线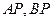 分别与椭圆相交于异于
分别与椭圆相交于异于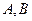 的点
的点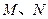 ,证明点
,证明点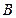 在以
在以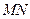 为直径的圆内.
为直径的圆内.
(此题不要求在答题卡上画图)
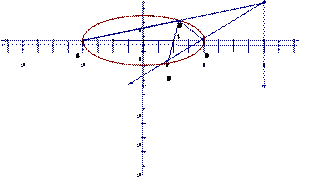
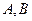 分别为椭圆
分别为椭圆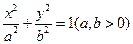 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且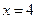 为它的右准线.
为它的右准线.(Ⅰ)求椭圆的方程;
(Ⅱ)设
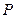 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线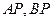 分别与椭圆相交于异于
分别与椭圆相交于异于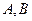 的点
的点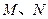 ,证明点
,证明点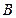 在以
在以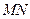 为直径的圆内.
为直径的圆内.(此题不要求在答题卡上画图)

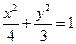
(I)依题意得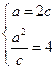 解得
解得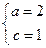 从而b=
从而b=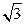 ,………………………………………3分
,………………………………………3分
故椭圆方程为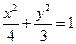 .……………………………………………………………………4分
.……………………………………………………………………4分
(II)解法1:由(I)得A(-2,0),B(2,0),设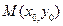 .
.
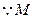 点在椭圆上,
点在椭圆上,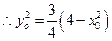 .……………………………………………………… 5分
.……………………………………………………… 5分
又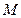 点异于顶点
点异于顶点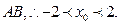
由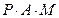 三点共线可得
三点共线可得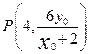 ,…………………………………………………………………6分
,…………………………………………………………………6分
从而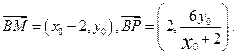 .……………………………………………………………7分
.……………………………………………………………7分
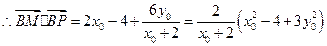 ,………………………………………………10分
,………………………………………………10分
将①式代入②式化简得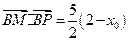 .…………………………………………………………12分
.…………………………………………………………12分
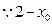 >0,
>0,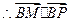 >0.于是
>0.于是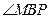 为锐角,从而
为锐角,从而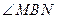 为钝角,
为钝角,
故点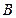 在以
在以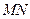 为直径的圆内.………………………………………………………………………. 14分
为直径的圆内.………………………………………………………………………. 14分
解法2:由(Ⅰ)得A(-2,0),B(2,0).设P(4,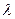 )(
)(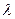
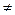 0),M(
0),M( ,
, ),N(
),N( ,
, ),则直线AP的方程为
),则直线AP的方程为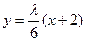 ,直线BP的方程为
,直线BP的方程为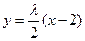 .…………………………….. 6分
.…………………………….. 6分
 点M、N分别在直线AP、BP上,
点M、N分别在直线AP、BP上,
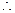
 =
=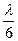 (
( +2),
+2), =
=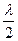 (
( -2).从而
-2).从而
 =
=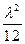 (
( +2)(
+2)( -2).③
-2).③
联立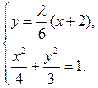 消去y得(27+
消去y得(27+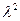 )
)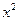 +4
+4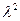 x+4(
x+4(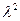 -27)=0………………8分
-27)=0………………8分

 ,-2是方程得两根,
,-2是方程得两根,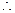 (-2).
(-2). ,即
,即 =
=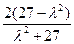 . ④
. ④
又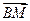 .
.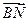 =(
=( -2,
-2,  ).(
).( -2,
-2, )=(
)=( -2)(
-2)( -2)+
-2)+
 . ⑤………9分
. ⑤………9分
于是由③、④式代入⑤式化简可得
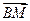 .
.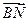 =
=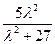 (
( -2)………………………………………………………… 12分
-2)………………………………………………………… 12分
 N点在椭圆上,且异于顶点A、B,
N点在椭圆上,且异于顶点A、B,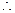
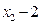 <0.
<0.
又
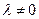 ,
,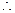
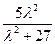 > 0, 从而
> 0, 从而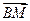 .
.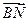 <0.
<0.
故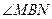
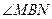 为钝角,即点B在以MN为直径的圆内………………………………14分
为钝角,即点B在以MN为直径的圆内………………………………14分
解法3:由(Ⅰ)得A(-2,0),B(2,0).设M( ,
, ),N(
),N( ,
, ),则-2<
),则-2< <2 , -2<
<2 , -2< <2.又MN的中点Q的坐标为(
<2.又MN的中点Q的坐标为(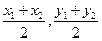 ),………………………………………5分
),………………………………………5分
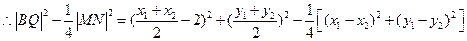
化简得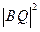 -
-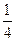
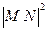 =(
=( -2)(
-2)( -2)+
-2)+
 . ⑥………………8分
. ⑥………………8分
直线AP的方程为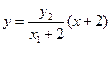 ,直线BP的方程为
,直线BP的方程为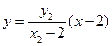 ………………10分
………………10分
 点P在准线x=4上,
点P在准线x=4上,
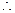
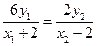 ,即
,即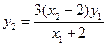 . ⑦
. ⑦
又 M点在椭圆上,
M点在椭圆上,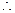
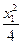 +
+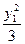 =1,即
=1,即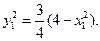 ⑧……… 12分
⑧……… 12分
于是将⑦、⑧式化简可得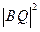 -
-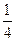
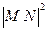 =
=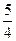
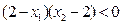 .
.
从而B在以MN为直径的圆内………………………………………………………………… 14分
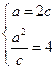 解得
解得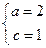 从而b=
从而b=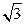 ,………………………………………3分
,………………………………………3分故椭圆方程为
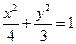 .……………………………………………………………………4分
.……………………………………………………………………4分(II)解法1:由(I)得A(-2,0),B(2,0),设
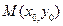 .
.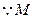 点在椭圆上,
点在椭圆上,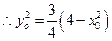 .……………………………………………………… 5分
.……………………………………………………… 5分又
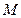 点异于顶点
点异于顶点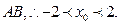
由
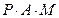 三点共线可得
三点共线可得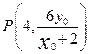 ,…………………………………………………………………6分
,…………………………………………………………………6分从而
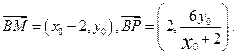 .……………………………………………………………7分
.……………………………………………………………7分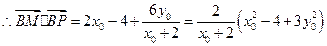 ,………………………………………………10分
,………………………………………………10分将①式代入②式化简得
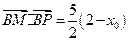 .…………………………………………………………12分
.…………………………………………………………12分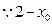 >0,
>0,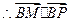 >0.于是
>0.于是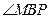 为锐角,从而
为锐角,从而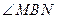 为钝角,
为钝角,故点
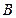 在以
在以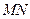 为直径的圆内.………………………………………………………………………. 14分
为直径的圆内.………………………………………………………………………. 14分解法2:由(Ⅰ)得A(-2,0),B(2,0).设P(4,
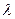 )(
)(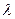
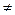 0),M(
0),M( ,
, ),N(
),N( ,
, ),则直线AP的方程为
),则直线AP的方程为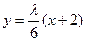 ,直线BP的方程为
,直线BP的方程为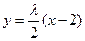 .…………………………….. 6分
.…………………………….. 6分 点M、N分别在直线AP、BP上,
点M、N分别在直线AP、BP上,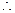
 =
=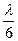 (
( +2),
+2), =
=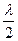 (
( -2).从而
-2).从而
 =
=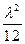 (
( +2)(
+2)( -2).③
-2).③联立
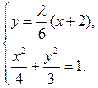 消去y得(27+
消去y得(27+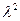 )
)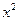 +4
+4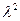 x+4(
x+4(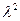 -27)=0………………8分
-27)=0………………8分
 ,-2是方程得两根,
,-2是方程得两根,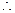 (-2).
(-2). ,即
,即 =
=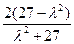 . ④
. ④又
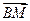 .
.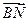 =(
=( -2,
-2,  ).(
).( -2,
-2, )=(
)=( -2)(
-2)( -2)+
-2)+
 . ⑤………9分
. ⑤………9分于是由③、④式代入⑤式化简可得
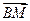 .
.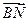 =
=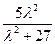 (
( -2)………………………………………………………… 12分
-2)………………………………………………………… 12分 N点在椭圆上,且异于顶点A、B,
N点在椭圆上,且异于顶点A、B,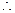
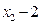 <0.
<0.又

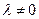 ,
,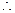
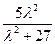 > 0, 从而
> 0, 从而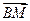 .
.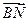 <0.
<0.故
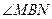
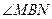 为钝角,即点B在以MN为直径的圆内………………………………14分
为钝角,即点B在以MN为直径的圆内………………………………14分解法3:由(Ⅰ)得A(-2,0),B(2,0).设M(
 ,
, ),N(
),N( ,
, ),则-2<
),则-2< <2 , -2<
<2 , -2< <2.又MN的中点Q的坐标为(
<2.又MN的中点Q的坐标为(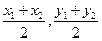 ),………………………………………5分
),………………………………………5分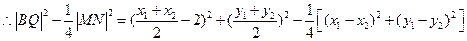
化简得
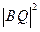 -
-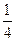
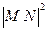 =(
=( -2)(
-2)( -2)+
-2)+
 . ⑥………………8分
. ⑥………………8分直线AP的方程为
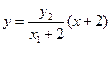 ,直线BP的方程为
,直线BP的方程为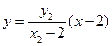 ………………10分
………………10分 点P在准线x=4上,
点P在准线x=4上,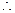
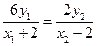 ,即
,即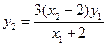 . ⑦
. ⑦又
 M点在椭圆上,
M点在椭圆上,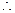
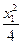 +
+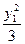 =1,即
=1,即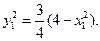 ⑧……… 12分
⑧……… 12分于是将⑦、⑧式化简可得
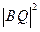 -
-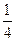
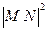 =
=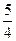
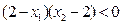 .
.从而B在以MN为直径的圆内………………………………………………………………… 14分

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
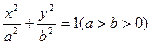 上一点,
上一点,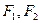 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足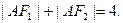
 轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
轴上,椭圆C上的点到焦点的最大值为3,最小值为1. :
: 与
与 椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线
椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线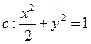 的两焦点为
的两焦点为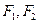 ,点
,点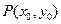 满足
满足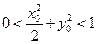 ,则|
,则|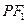 |+|
|+|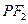 |的取值范围为_______,直线
|的取值范围为_______,直线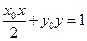 与椭圆C的公共点个数_____。
与椭圆C的公共点个数_____。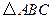 中,
中,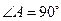 ,
,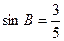 .若以
.若以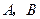 为焦点的椭圆经过点
为焦点的椭圆经过点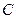 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )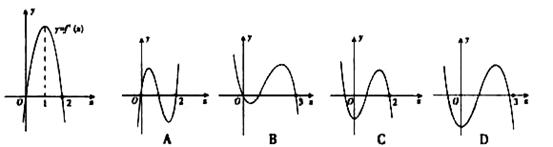
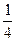
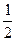
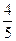
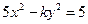 的一个焦点为(0,2),则
的一个焦点为(0,2),则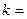 ( )
( )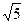
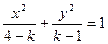 给出下面四个命题:
给出下面四个命题: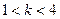 时,曲线C表示椭圆;
时,曲线C表示椭圆;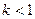 或
或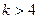
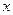 轴上的椭圆,则
轴上的椭圆,则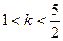
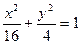 的离心率为 .
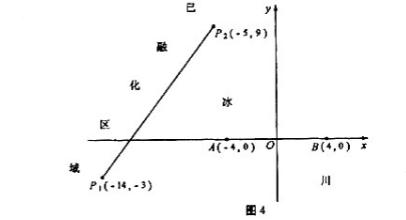
的离心率为 . 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?