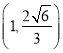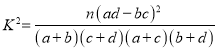题目内容
【题目】已知椭圆
的右焦点为
，右顶点为
，离心离为
，点
满足条件
．
（Ⅰ）求
的值．
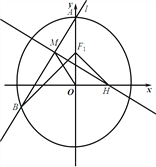
（Ⅱ）设过点
的直线
与椭圆
相交于
、
两点，记
和
的面积分别为
、
，求证： 
．
【答案】（Ⅰ）
（Ⅱ）见解析
【解析】试题分析：（Ⅰ）解：因为椭圆C的方程为
，根据椭圆的性质和数据建立方程即可求出结果；
（Ⅱ）若直线l的斜率不存在， 则有
， 
，符合题意.
若直线l的斜率存在，则设直线l的方程为
，
，
.
由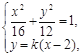
得
，可知
恒成立，且
，
. 因为
，所以
.
因为
和
的面积分别为
， 
， 即可得证.
试题解析：（Ⅰ）解：因为椭圆C的方程为
，
所以
, 
, 
, 2分
则
， 
， 
. 3分
因为
，
所以
. 5分
（Ⅱ）解：若直线l的斜率不存在， 则有， 
，符合题意. 6分
若直线l的斜率存在，则设直线l的方程为，，.
由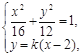
得
， 7分
可知恒成立，且，. 8分
因为
10分
，
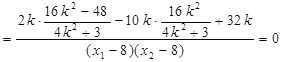所以
. 12分
因为
和
的面积分别为
，
， 13分
所以
. 14分.
练习册系列答案
相关题目
