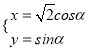Question

【题目】已知函数，其中， ．

（Ⅰ）当时， 的零点为______；（将结果直接填写在横线上）

（Ⅱ）当时，如果存在，使得，试求的取值范围；

（Ⅲ）如果对于任意，都有成立，试求的最大值．

Answer 1

【答案】（Ⅰ）零点；（Ⅱ）；（Ⅲ）．

【解析】试题分析：（Ⅰ）解一元二次方程可得零点（Ⅱ）根据a分类讨论：一次函数必存在负值，开口向下的二次函数必存在负值，只需研究开口向上的二次函数有负值的条件，即判别式大于零，解不等式可得的取值范围；（Ⅲ）根据二次函数实根分布得关于a,b不等式，作出可行域，再根据线性规划求的最大值．

试题解析：（Ⅰ）当时， ，所以

（Ⅱ）当时，满足题意；当时，由得 ，即，综上可得的取值范围为

（Ⅲ）由题意得 ，作可行域如图，则直线 过点A(1，1)时取最大值2，即的最大值为2.