题目内容
 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队抽6人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队抽6人.(1)求n的值;
(2)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
考点:程序框图
专题:计算题,算法和程序框图
分析:(1)根据分层抽样可得
=
,故可求n的值;
(2)确定满足0≤x≤1,0≤y≤1点的区域,由条件
得到的区域为图中的阴影部分,计算面积,可求该代表中奖的概率.
| 6 |
| 120 |
| 20 |
| 120+120+n |
(2)确定满足0≤x≤1,0≤y≤1点的区域,由条件
|
解答:
解:(1)∵由题意可得
=
,∴可解得n=160;
(2)由已知0≤x≤1,0≤y≤1,点(x,y)在如图所示的正方形OABC内,
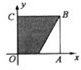
由条件
得到的区域为图中的阴影部分
由2x-y-1=0,令y=0可得x=
,令y=1可得x=1
∴在x,y∈[0,1]时满足2x-y-1≤0的区域的面积为S阴影=
×(1+
)×1=
,
∴该代表中奖的概率为
=
.
| 6 |
| 120 |
| 20 |
| 120+120+n |
(2)由已知0≤x≤1,0≤y≤1,点(x,y)在如图所示的正方形OABC内,

由条件
|
由2x-y-1=0,令y=0可得x=
| 1 |
| 2 |
∴在x,y∈[0,1]时满足2x-y-1≤0的区域的面积为S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∴该代表中奖的概率为
| ||
| 1 |
| 3 |
| 4 |
点评:本题主要考察了程序框图和算法,考查概率与统计知识,考查分层抽样,考查概率的计算,确定概率的类型是关键,本题属于基本知识的考查.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
数列{an}满足an+2an=2an+1(n∈N*),且a1=1,a2=2,则数列{an}的前2014项的乘积为( )
| A、22012 |
| B、22013 |
| C、22014 |
| D、22015 |

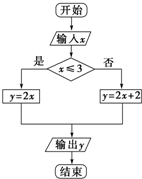 根据如图的框图回答后面的问题.
根据如图的框图回答后面的问题.