题目内容
在平面直角坐标系xOy中,曲线y=x2-4x+3与坐标轴的交点都在圆C上.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x+y+m=0交于A,B两点,且
⊥
,求m的值.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x+y+m=0交于A,B两点,且
| OA |
| OB |
考点:直线和圆的方程的应用,二次函数的性质
专题:综合题,直线与圆
分析:(Ⅰ)求出曲线y=x2-4x+3与y轴的交点为(0,3),与x轴的交点为(1,0),(3,0),确定圆心与半径,即可求圆C的方程;
(Ⅱ)联立方程得到方程组,消元得到2x2+2mx+m2+4m+3=0,由韦达定理得x1x2,y1y2再由x1x2+y1y2=0,代入可求解.
(Ⅱ)联立方程得到方程组,消元得到2x2+2mx+m2+4m+3=0,由韦达定理得x1x2,y1y2再由x1x2+y1y2=0,代入可求解.
解答:
解:(Ⅰ)曲线y=x2-4x+3与y轴的交点为(0,3),与x轴的交点为(1,0),(3,0),
故可设C的圆心为(2,t),则有(2-0)2+(t-3)2=(2-1)2+(t-0)2解得t=2,
则圆C的半径为
=
所以圆C的方程为(x-2)2+(y-2)2=5.…(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),
,
消去y,得到方程2x2+2mx+m2+4m+3=0,…(6分)
由已知可得,判别式△=4m2-4×2(m2+4m+3)>0,化简得m2+8m+6<0,…(7分)
x1+x2=m,x1x2=
①…(8分)
由于
⊥
,可得x1x2+y1y2=0…(9分)
又y1=-x1-m,y2=-x2-m所以2x1x2+m(x1+x2)+m2=0②…(10分)
由①,②得m=-1或m=-3,满足△>0,
故m=-1或m=-3.…(12分)
故可设C的圆心为(2,t),则有(2-0)2+(t-3)2=(2-1)2+(t-0)2解得t=2,
则圆C的半径为
| (2-1)2+22 |
| 5 |
所以圆C的方程为(x-2)2+(y-2)2=5.…(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),
|
消去y,得到方程2x2+2mx+m2+4m+3=0,…(6分)
由已知可得,判别式△=4m2-4×2(m2+4m+3)>0,化简得m2+8m+6<0,…(7分)
x1+x2=m,x1x2=
| m2+4m+3 |
| 2 |
由于
| OA |
| OB |
又y1=-x1-m,y2=-x2-m所以2x1x2+m(x1+x2)+m2=0②…(10分)
由①,②得m=-1或m=-3,满足△>0,
故m=-1或m=-3.…(12分)
点评:本题考查直线与圆的位置关系,注意韦达定理及整体思想的运用,属中档题.

练习册系列答案
相关题目
函数y=2x-x2的图象大致是( )
A、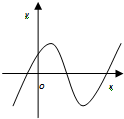 |
B、 |
C、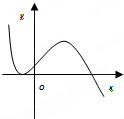 |
D、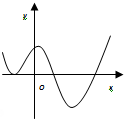 |
如图,Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是( )

A、
| ||||
| B、1 | ||||
C、
| ||||
D、2
|
设数列{an}的前n项和为Sn,a1=1,an=
+2(n-1)(n∈N*),若S1+
+
+…+
-(n-1)2=4027,则n的值为( )
| Sn |
| n |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
| A、4027 | B、2013 |
| C、2014 | D、4026 |
 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队抽6人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队抽6人.