题目内容
【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B. 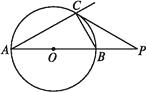
(1)试探索∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么关系?
(3)∠A可能等于45°吗?为什么?
【答案】
(1)解:∵PC是切线,
∴∠BCP=∠A.
又∵AB是直径,
∴∠ACB=90°.
在△ACP中,∠A+∠P+∠ACP=180°,
∴∠BCP+∠P+∠ACB+∠BCP=180°.
∴2∠BCP+∠P+90°=180°.
∴∠P=90°-2∠BCP.
(2)解:若∠A=30°,则∠BCP=∠A=30°,∠ABC=60°.
∴∠P=30°,∴PB=BC,BC= AB.
∴PB= PA,即PA=3PB.
(3)解:∠A不可能等于45°.
原因:设∠A=45°,则∠ABC=45°,∠BCP=45°,
∴CP∥AB,与题干中PC与AB交于点P矛盾,
∴∠A不可能等于45°.
【解析】本题主要考查了弦切角的性质,解决问题的关键是根据弦切角的性质结合所给几何条件分析计算即可解决问题,有一定难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗?
总成绩好 | 总成绩不好 | 总计 | |
数学成绩好 | 20 | 10 | 30 |
数学成绩不好 | 5 | 15 | 20 |
总计 | 25 | 25 | 50 |
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)