题目内容
【题目】已知 
是R上的增函数，则a的取值范围是 ．
【答案】[2，+∞）
【解析】解：首先，y=logax在区间[1，+∞）上是增函数
且函数y=（a+2）x﹣2a区间（﹣∞，1）上也是增函数
∴a＞1…（1）
其次在x=1处函数对应的第一个表达式的值要小于或等于第二个表达式的值，即
（a+2）﹣2a≤loga1a≥2…（2）
联解（1）、（2）得a≥2．
所以答案是：[2，+∞）．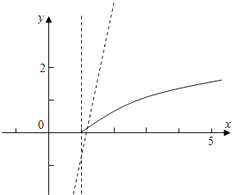
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识，掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集，以及对对数函数的单调性与特殊点的理解，了解过定点（1，0），即x=1时，y=0;a>1时在（0，+∞）上是增函数;0>a>1时在（0，+∞）上是减函数．
练习册系列答案
相关题目
