题目内容
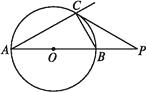
【题目】轴截面是边长为4 
的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为 
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为（ ）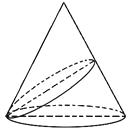 
A.
B.
C.
D.
【答案】C
【解析】解答：本题综合考查空间几何体中的线面关系与解析几何中直线与直线的位置关系以及平面几何中圆的相关定理的应用,意在考查数形结合思想与空间想象能力.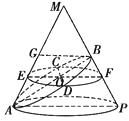 
如图,根据轴截面是边长为4 
的等边三角形,可知椭圆的长轴长为AB=6,设O为椭圆的中心,则a=OB=OA=3,过O作平行于底面的平面,可得到截面圆,交椭圆于两点C、D,则C、D即是椭圆短半轴的顶点.根据题意知AB⊥BF,在直角三角形OBF中,∠OBF=90°，所以FO=2 ,F是BP的中点,过点B作AP的平行线,交AM于点G,则E是AG的中点,所以OE= 
AP= ,由相交弦定理得CO2=OF×OE,所以b2=6,所以c2=a2-b2=3,所以椭圆的离心率为 
.
分析：本题主要考查了平面与圆锥面的截线，解决问题的关键是根据平面与圆锥面的截线满足的有关条件通过构造辅助线结合所学椭圆性质及相交弦定理计算即可
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示：
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
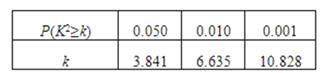
参考公式及数据：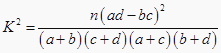 
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
（1）如果随机抽查这个班的一名学生，那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？
（2）试运用独立性检验的思想方法分析：学生的学习积极性与对待班级工作的态度是否有关系？并说明理由？
