题目内容
已知f(x)=
,则f(x)( )
| ||
| |x+2|-2 |
| A.是奇函数 | B.是偶函数 |
| C.既是奇函数又是偶函数 | D.是非奇非偶函数 |
由于已知f(x)=
=
由
,求得它的定义域为{x|-1≤x≤1,且x≠0},满足关于原点对称,
∴f(x)=
.
再根据它满足f(-x)=
=-
=-f(x),故函数为奇函数,
故选A.
| ||
| |x+2|-2 |
由
|
∴f(x)=
| ||
| x |
再根据它满足f(-x)=
| ||
| -x |
| ||
| x |
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
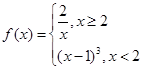 若关于
若关于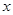 的方程
的方程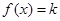 有两个不同的实根,则实数
有两个不同的实根,则实数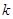 的取值范围是________.
的取值范围是________.